【题目】探索研究.请解决下列问题:
(1)已知△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,并把所有不同的分割方法都画出来,图不够可以自己画.只需画图,不必说明理由,但要在图中标出相等两角的度数).
(2)已知等腰△ABC中,AB=AC,D为BC上一点,连接AD,若△ABD和△ACD都是等腰三角形,则∠B的度数为 (请画出示意图,并标明必要的角度).
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
试题分析:(1)由∠A=90°,∠B=67.5°,则∠C=22.5°,要使分割成的两个三角形为等腰三角形,必须要得出一个角为22.5°,或另一个角为67.5,因此需要把90°的角或67.5°的角得出22.5,从这两个角入手分出22.5°的角解决问题;
(2)要使分成的△ABD和△ACD都是等腰三角形,首先想到等腰直角三角形,再次想到“黄金三角形”,由此得出答案即可.
解:(1)如图,
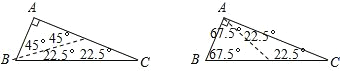
(2)如图,
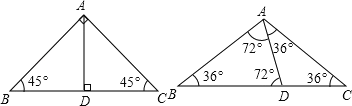
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( )个
①三个内角对应相等的两个三角形全等;
②三条边对应相等的两个三角形全等;
③有两角和一边分别对应相等的两个三角形全等;
④等底等高的两个三角形全等.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2
 ;③tan∠DCF=
;③tan∠DCF=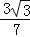 ;④△ABF的面积为
;④△ABF的面积为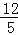
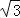 .其中一定成立的是 (把所有正确结论的序号都填在横线上).
.其中一定成立的是 (把所有正确结论的序号都填在横线上).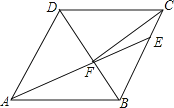
-
科目: 来源: 题型:
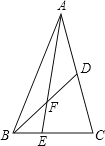
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF= .
-
科目: 来源: 题型:
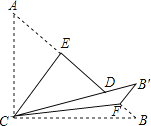
查看答案和解析>>【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边Ac沿CE翻折,使点A落在AB上的D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点F处,两条折痕与斜边AB分别交于点E、F,则线段BF的长为( )
A.
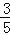 B.
B. C.
C.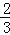 D.
D.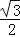
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=3,则a2﹣2ab+b2﹣6的值是( )
A. 12 B. 6 C. 3 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣a)7÷(﹣a)4×(﹣a)3
(2)a3(﹣b3)2+(﹣2ab2)3
(3)2(a2)3﹣a2
 a4+(2a4)2÷a2
a4+(2a4)2÷a2(4)(
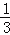 )﹣3﹣(3.14﹣π)0+(﹣2)4.
)﹣3﹣(3.14﹣π)0+(﹣2)4.
相关试题

