【题目】(2016黑龙江省哈尔滨市)已知:△ABC内接于⊙O,D是![]() 上一点,OD⊥BC,垂足为H.
上一点,OD⊥BC,垂足为H.
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;
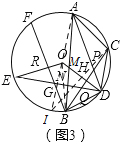
(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=![]() ,BN=
,BN=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求BF的长.
,求BF的长.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)24.
【解析】试题分析:(1)OD⊥BC可知点H是BC的中点,又中位线的性质可得AC=2OH;
(2)由垂径定理可知:![]() ,所以∠BAD=∠CAD,由因为∠ABC=∠ADC,所以∠ACD=∠APB;
,所以∠BAD=∠CAD,由因为∠ABC=∠ADC,所以∠ACD=∠APB;
(3)由∠ACD﹣∠ABD=2∠BDN可知∠AND=90°,由tan∠ABC=![]() 可知NQ和BQ的长度,再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC,所以BG=BQ,连接AO并延长交⊙O于点I,连接IC后利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=
可知NQ和BQ的长度,再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC,所以BG=BQ,连接AO并延长交⊙O于点I,连接IC后利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=![]() 即可求得RG的长度,最后由垂径定理可求得BF的长度.
即可求得RG的长度,最后由垂径定理可求得BF的长度.
试题解析:(1)∵OD⊥BC,∴由垂径定理可知:点H是BC的中点,∵点O是AB的中点,∴OH是△ABC的中位线,∴AC=2OH;
(2)∵OD⊥BC,∴由垂径定理可知:![]() ,∴∠BAD=∠CAD,∵
,∴∠BAD=∠CAD,∵![]() ,∴∠ABC=∠ADC,∴180°﹣∠BAD﹣∠ABC=180°﹣∠CAD﹣∠ADC,∴∠ACD=∠APB,(3)连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,∵∠ACD﹣∠ABD=2∠BDN,∴∠ACD﹣∠BDN=∠ABD+∠BDN,∵∠ABD+∠BDN=∠AND,∴∠ACD﹣∠BDN=∠AND,∵∠ACD+∠ABD=180°,∴∠ABD+∠BDN=180°﹣∠AND,∴∠AND=180°﹣∠AND,∴∠AND=90°,∵tan∠ABC=
,∴∠ABC=∠ADC,∴180°﹣∠BAD﹣∠ABC=180°﹣∠CAD﹣∠ADC,∴∠ACD=∠APB,(3)连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,∵∠ACD﹣∠ABD=2∠BDN,∴∠ACD﹣∠BDN=∠ABD+∠BDN,∵∠ABD+∠BDN=∠AND,∴∠ACD﹣∠BDN=∠AND,∵∠ACD+∠ABD=180°,∴∠ABD+∠BDN=180°﹣∠AND,∴∠AND=180°﹣∠AND,∴∠AND=90°,∵tan∠ABC=![]() ,BN=
,BN=![]() ,∴NQ=
,∴NQ=![]() ,∴由勾股定理可求得:BQ=
,∴由勾股定理可求得:BQ=![]() ,∵∠BNQ=∠QHD=90°,∴∠ABC=∠QDH,∵OE=OD,∴∠OED=∠QDH,∵∠ERG=90°,∴∠OED=∠GBN,∴∠GBN=∠ABC,∵AB⊥ED,∴BG=BQ=
,∵∠BNQ=∠QHD=90°,∴∠ABC=∠QDH,∵OE=OD,∴∠OED=∠QDH,∵∠ERG=90°,∴∠OED=∠GBN,∴∠GBN=∠ABC,∵AB⊥ED,∴BG=BQ=![]() ,GN=NQ=
,GN=NQ=![]() ,∵AI是⊙O直径,∴∠ACI=90°,∵tan∠AIC=tan∠ABC=
,∵AI是⊙O直径,∴∠ACI=90°,∵tan∠AIC=tan∠ABC=![]() ,∴
,∴![]() =
=![]() ,∴IC=
,∴IC=![]() ,∴由勾股定理可求得:AI=25,连接OB,设QH=x,∵tan∠ABC=tan∠ODE=
,∴由勾股定理可求得:AI=25,连接OB,设QH=x,∵tan∠ABC=tan∠ODE=![]() ,∴
,∴![]() =
=![]() ,∴HD=2x,∴OH=OD﹣HD=
,∴HD=2x,∴OH=OD﹣HD=![]() ﹣2x,BH=BQ+QH=
﹣2x,BH=BQ+QH=![]() +x,由勾股定理可得:
+x,由勾股定理可得:![]() ,∴
,∴![]() ,解得:x=
,解得:x=![]() 或x=
或x=![]() .
.
①当QH=![]() 时,∴QD=
时,∴QD=![]() QH=
QH=![]() ,∴ND=QD+NQ=
,∴ND=QD+NQ=![]() ,∴MN=
,∴MN=![]() ,MD=15.∵MD>
,MD=15.∵MD>![]() ,∴QH=
,∴QH=![]() 不符合题意,舍去;
不符合题意,舍去;
②当QH=![]() 时,∴QD=
时,∴QD=![]() QH=
QH=![]() ,∴ND=NQ+QD=
,∴ND=NQ+QD=![]() ,由垂径定理可求得:ED=
,由垂径定理可求得:ED=![]() ,∴GD=GN+ND=
,∴GD=GN+ND=![]() ,∴EG=ED﹣GD=
,∴EG=ED﹣GD=![]() ,∵tan∠OED=
,∵tan∠OED=![]() ,∴
,∴![]() =
=![]() ,∴EG=
,∴EG=![]() RG,∴RG=
RG,∴RG=![]() ,∴BR=RG+BG=12,∴由垂径定理可知:BF=2BR=24.
,∴BR=RG+BG=12,∴由垂径定理可知:BF=2BR=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
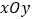 中,函数
中,函数 的图象与直线
的图象与直线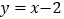 交于点
交于点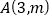 .
.(1)求
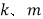 的值;
的值;(2)已知点
 ,过点
,过点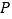 作平行于
作平行于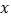 轴的直线,交直线
轴的直线,交直线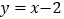 于点
于点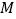 ,过点
,过点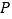 作平行于
作平行于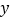 轴的直线,交函数
轴的直线,交函数 的图象于点
的图象于点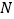 .
.①当
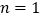 时,判断线段
时,判断线段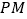 与
与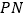 的数量关系,并说明理由;
的数量关系,并说明理由;②若
 ,结合函数的图象,直接写出
,结合函数的图象,直接写出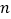 的取值范围.
的取值范围.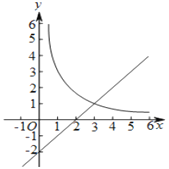
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在平面直角坐标系
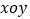 中,直线
中,直线 分别交
分别交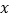 轴、
轴、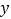 轴于点
轴于点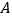 、
、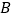 两点,直线
两点,直线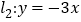 过原点且与直线
过原点且与直线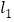 相交于
相交于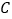 ,点
,点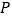 为
为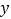 轴上一动点.
轴上一动点.(1)求点
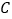 的坐标;
的坐标;(2)求出
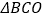 的面积;
的面积;(3)当
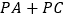 的值最小时,求此时点
的值最小时,求此时点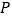 的坐标;
的坐标;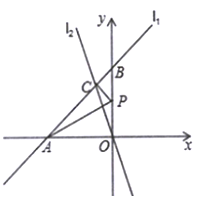
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2
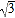 ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )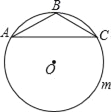
A. y=
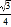 x+4 B. y=
x+4 B. y=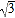 x+4 C. y=
x+4 C. y=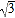 x2+4 D. y=
x2+4 D. y=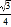 x2+4
x2+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形
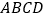 中,
中,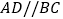 ,
,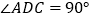 ,
,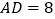 ,
,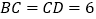 ,点
,点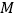 从点
从点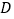 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点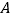 运动,同时,点
运动,同时,点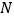 从点
从点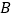 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点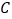 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点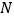 作
作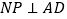 于点
于点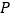 ,连接
,连接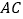 交
交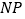 于点
于点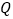 ,连接
,连接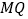 ,设运动时间为
,设运动时间为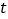 秒.
秒.(1)连接
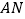 、
、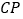 ,当
,当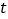 为何值时,四边形
为何值时,四边形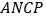 为平行四边形;
为平行四边形;(2)求出点
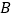 到
到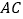 的距离;
的距离;(3)如图2,将
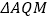 沿
沿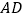 翻折,得
翻折,得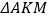 ,是否存在某时刻
,是否存在某时刻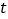 ,使四边形
,使四边形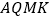 为菱形,若存在,求
为菱形,若存在,求 的值;若不存在,请说明理由
的值;若不存在,请说明理由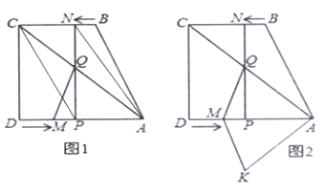
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
相关试题

