【题目】在![]() 中,以
中,以![]() 为斜边,作直角
为斜边,作直角![]() ,使点
,使点![]() 落在
落在![]() 内,
内, ![]() .
.
(1)如图1,若![]() ,
, ![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 、
、![]() 边的中点,连接
边的中点,连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)如图2,若![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转一定角度,得到
逆时针旋转一定角度,得到![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证: ![]() ;
;
(3)如图3,若![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
, ![]() ,且
,且![]() ,请直接写出线段
,请直接写出线段![]() 之间的关系(不需要证明).
之间的关系(不需要证明).

参考答案:
【答案】(1)PM=7;(2)证明见解析;(3)BP=CP
【解析】试题分析:(1)根据直角三角形30度角性质求出AB,再根据三角形中位线定理即可求出PM.
(2)如图2中,在ED上截取EQ=DP,连接CQ.首先证明△EQC≌△DPB,推出QC=PB,再证明QC=PC即可解决问题.
(3)结论:2AD2=FB2+CF2.如图3中,连接AF交BD于N.由△AND∽△BNF,推出![]() ,推出
,推出![]() ,又∠ANB=∠DNF,推出△ANB∽△DNF,从∠DFN=∠ABD=45°,在RtABF中利用勾股定理即可证明.
,又∠ANB=∠DNF,推出△ANB∽△DNF,从∠DFN=∠ABD=45°,在RtABF中利用勾股定理即可证明.
试题解析:(1)如图1中,
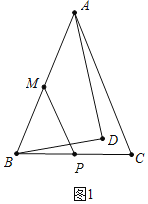
∵∠ADB=90°,∠DBA=60°,AD=![]() ,
,
∴∠BAD=30°,
∴AB=2BD,设BD=a,则AB=2a,
∵AB2=BD2+AD2,
∴(2a)2=a2+(![]() )2,
)2,
∴a=7,
∴AB=AC=14,
∵AM=MB,PB=PC,
∴PM=![]() AC=7.
AC=7.
(2)证明:如图2中,在ED上截取EQ=DP,连接CQ.
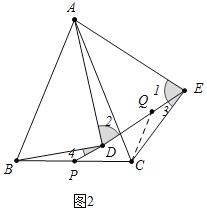
∵AD=AE,
∴∠1=∠2,
∵∠ADB=∠AEC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∵BD=EC,
∴△EQC≌△DPB,
∴CQ=BP,∠QCE=∠DBP,
∵∠CQP=∠3+∠QCE,∠CPQ=∠4+∠DBP,
∴∠CQP=∠CPQ,
∴CQ=PC,
∴PB=PC.
(3)结论:2AD2=FB2+CF2.
理由:如图3中,连接AF交BD于N.
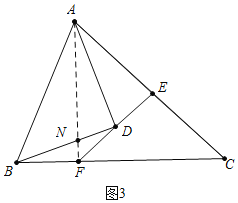
∵∠ADB=90°,DA=DB,
∴∠DBA=∠DAB=45°,AB=![]() AD,
AD,
∵∠AND=∠BNF,∠ADN=∠BFN=90°,
∴△AND∽△BNF,
∴![]() ,
,
∴![]() ,
,
∵∠ANB=∠DNF,
∴△ANB∽△DNF,
∴∠DFN=∠ABD=45°,
∵FE⊥AC,AE=EC,
∴FA=FC,∠AFE=∠CFE=45°,
∴∠AFC=∠AFB=90°,
∴AB2=BF2+AF2,
∴2AD2=BF2+CF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】备战中考,初三的学子们感觉到严重的睡眠不足,经抽样调查了同学们的睡眠时间,制成了如下两幅统计图:

请根据两幅图形解决下列问题:
(1)将条形统计图补充完整;求扇形统计图中B代表的扇形的圆心角是________
(2)睡眠时间的中位数是_______
(3)如果把睡眠时间低于7小时称为严重睡眠不足,请估算全校2800个初三同学中睡眠严重不足的人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】与﹣3x2y是同类项的是( )
A.﹣2x2y
B.﹣3xy2
C.2x3y
D.5xy -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是□APQM面积的
 时,求□APQM面积.
时,求□APQM面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在某时刻以每件60元的价格卖出一件衣服,盈利25%,则这件衣服的进价是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )

A. 6 B. 7 C. 8 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2015=( )
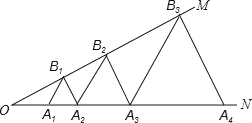
A. 22013 B. 22014 C. 22015 D. 22016
相关试题

