搜索
【题目】已知一次函数的图象与直线y=﹣x+1平行，且过点（8，2），那么此一次函数的解析式为 ．
参考答案：
【答案】y=－x+10
【解析】
由函数的图象与直线y=-x+1平行，可得斜率，将点（8，2）代入即可人求解．
解：设所求一次函数的解析式为 y=kx+b，
∵函数的图象与直线y=-x+1平行，
∴k=-1，
又过点（8，2），有2=-1×8+b，
解得b=10，
∴一次函数的解析式为y=-x+10，
故答案为：y=-x+10．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）
如图，已知AB∥CD，BE、CF分别平分∠ABC和∠DCB，求证：BE∥CF．
证明：∵AB∥CD，（已知）
∴∠_______＝∠_______．(_________________________)
∵__________________________________________，（已知）
∴∠EBC＝
_______，（角平分线定义）同理，∠FCB＝______________．
∴∠EBC＝∠FCB．（等式性质）
∴BE//CF．( ____________________________)
-
科目： 来源： 题型：
查看答案和解析>>【题目】试解答下列问题：
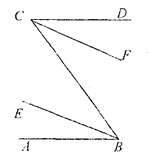
(1)在图1我们称之为“8字形”，请直接写出∠A、∠B、∠C、∠D之间的数量关系： ；
(2)仔细观察，在图2中“8字形”的个数是 个；
(3) 在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试求∠P的度数；
(4)如果图2中∠D和∠B为任意角时，其他条件不变，试写出∠B与∠P、∠D之间数量关系 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“等角的补角相等”的条件是_____，结论是_____．
-
科目： 来源： 题型：
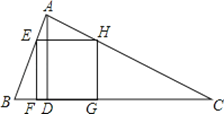
查看答案和解析>>【题目】如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．
（1）求证：△AEH∽△ABC；
（2）求这个正方形的边长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，点P（1，0）．点P第1次向上跳动1个单位至点P1（1，1），紧接着第2次向左跳动2个单位至点P2（－1，1），第3次向上跳动1个单位至点P3，第4次向右跳动3个单位至点P4，第5次又向上跳动1个单位至点P5，第6次向左跳动4个单位至点P6，……．照此规律，点P第100次跳动至点P100的坐标是（ ）
A. （－26，50） B. （－25，50） C. （26，50） D. （25，50）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD⊥BC于D，AE平分∠BAC．
（1）若∠C=70°，∠B＝40°，求∠DAE的度数
（2）若∠C－∠B＝30°，则∠DAE＝________．
（3）若∠C－∠B＝
（∠C＞∠B），求∠DAE的度数（用含的代数式表示）．
相关试题
