【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
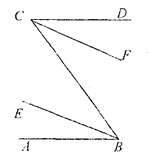
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=![]() _______,(角平分线定义)
_______,(角平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
参考答案:
【答案】答案见解析
【解析】证明:∵AB∥CD,(已知)
∴∠_ABC__=∠__DCB__.(__两直线平行,内错角相等__)
∵____ BE、CF分别平分∠ABC和∠DCB ___,(已知)
∴∠EBC=![]() _∠ABC_,(角平分线定义)
_∠ABC_,(角平分线定义)
同理,∠FCB=_![]() _∠DCB_,_.
_∠DCB_,_.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( _内错角相等,两直线平行__)
-
科目: 来源: 题型:
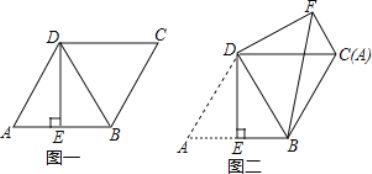
查看答案和解析>>【题目】如图一,菱形ABCD的边长为2,点E是AB的中点,且DE⊥AB.
(1)求证:△ABD是等边三角形;
(2)将图一中△ADE绕点D逆时针旋转,使得点A和点C重合,得到△CDF,连接BF,如图二,求线段BF的长.
-
科目: 来源: 题型:
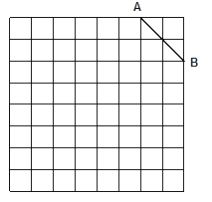
查看答案和解析>>【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(2,4),B点坐标为(4,2);
⑵ 请在(1)中建立的平面直角坐标系的第一象限内的格点上确定点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是 , △ABC的周长是 (结果保留根号);
⑶ 以(2)中△ABC的点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中, BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若
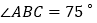 ,
,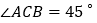 ,求∠D的度数;
,求∠D的度数;(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
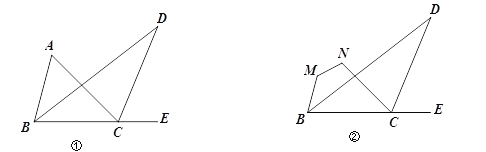
-
科目: 来源: 题型:
查看答案和解析>>【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】“等角的补角相等”的条件是_____,结论是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为 .
相关试题

