【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C-∠B=30°,则∠DAE=________.
(3)若∠C-∠B=![]() (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含![]() 的代数式表示).
的代数式表示).

参考答案:
【答案】(1)15°;(2)15°;(3)![]()
【解析】试题分析:(1)根据角平分线的定义和互余进行计算;
(2)根据三角形内角和定理和角平分线定义得出∠DAE的度数等于∠B与∠C差的一半解答即可;
(3)根据(2)中所得解答即可.
解:(1)由已知可得,∠BAC=180°﹣40°﹣70°=70°,
∴∠CAD=20°,
∴∠DAE=∠CAE﹣∠CAD=35°﹣20°=15°;
(2)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)=90°﹣
(180°﹣∠B﹣∠C)=90°﹣![]() (∠B+∠C),
(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°﹣![]() (∠B+∠C)﹣(90°﹣∠B)=
(∠B+∠C)﹣(90°﹣∠B)=![]() (∠B﹣∠C),
(∠B﹣∠C),
∵∠B﹣∠C=30°,
∴∠DAE=![]() ×30°=15°,
×30°=15°,
故答案为:15°;
(3)∵∠B﹣∠C=α,
∴∠DAE=![]() ×α=
×α=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为 .
-
科目: 来源: 题型:
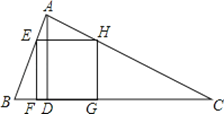
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
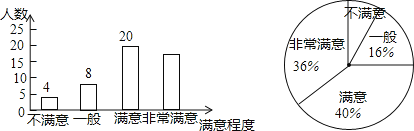
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某学校七至九年级学生每天的体育锻炼时间,下列抽样调查的样本代表性较好的是
A. 选择七年级一个班进行调查
B. 选择八年级全体学生进行调查
C. 选择全校七至九年级学号是5的整数倍的学生进行调查
D. 对九年级每个班按5%的比例用抽签的方法确定调查者
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,计算结果是x2+7x -18的是( )
A.(x-1)(x+18)
B.(x+2)(x+9)
C.(x-3)(x+6)
D.(x-2)(x+9)
相关试题

