【题目】如图,在每个小正方形的边长为![]() 的网格中,点
的网格中,点![]() ,
, ![]() ,
, ![]() 均在格点上.
均在格点上.

(Ⅰ)![]() 的面积等于____________;
的面积等于____________;
(Ⅱ)若四边形![]() 是正方形,且点
是正方形,且点![]() ,
, ![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,请在如图所示的网格中,用无刻度的直尺,画出点
上,请在如图所示的网格中,用无刻度的直尺,画出点![]() ,点
,点![]() ,并简要说明点
,并简要说明点![]() ,点
,点![]() 的位置是如何找到的(不要求证明)_____________.
的位置是如何找到的(不要求证明)_____________.
参考答案:
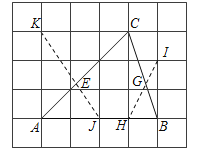
【答案】 6 取格点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .取格点
.取格点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .点
.点![]() ,
, ![]() 即为所求.
即为所求.
【解析】解:(Ⅰ)4×3÷2=6.故△ABC的面积等于6.
(Ⅱ)如图,取格点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .取格点
.取格点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .点
.点![]() ,
, ![]() 即为所求.
即为所求.
故答案为:(Ⅰ)6;(Ⅱ)如图,取格点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .取格点
.取格点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .点
.点![]() ,
, ![]() 即为所求.
即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求
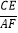 的值.
的值.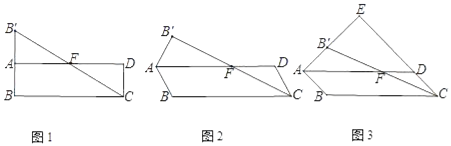
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减(辆)
-1
+3
-2
-4
+7
-5
-10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数
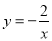 (x<0)的图像上,将此矩形向右平移3个单位长度到
(x<0)的图像上,将此矩形向右平移3个单位长度到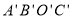 的位置,此时点
的位置,此时点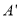 在函数
在函数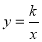 (x>0)的图像上,
(x>0)的图像上,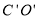 与此图像交于点P,则点P的坐标是_________.
与此图像交于点P,则点P的坐标是_________.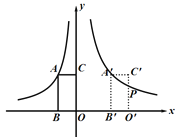
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
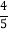 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△
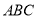 中,
中, 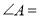 68°,以
68°,以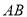 为直径的⊙
为直径的⊙ 与
与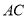 ,
, 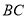 的交点分别为
的交点分别为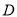 ,
, 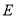 ,
, (Ⅰ)如图①,求
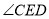 的大小;
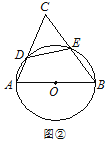
的大小;(Ⅱ)如图②,当
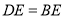 时,求
时,求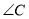 的大小.
的大小.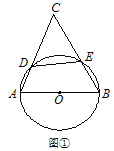
相关试题

