搜索
【题目】如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠PEF=30°，则∠EPF的度数是（ ）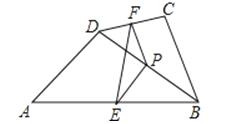
A.120°
B.150°
C.135°
D.140°
参考答案：
【答案】A
【解析】解：∵在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，
∴FP，PE分别是△CDB与△DAB的中位线，
∴PF=
BC，PE=AD，
∵AD=BC，
∴PF=PE，
故△EPF是等腰三角形．
∵∠PEF=30°，
∴∠PEF=∠PFE=30°，
∴∠EPF=120°．
故选A．
【考点精析】认真审题，首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半)．
-
科目： 来源： 题型：
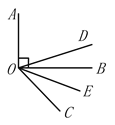
查看答案和解析>>【题目】如图，DO平分∠AOC，OE平分∠BOC，若OA⊥OB，
（1）当∠BOC＝30°，∠DOE＝_______________； 当∠BOC＝60°，∠DOE＝_______________；
（2）通过上面的计算，猜想∠DOE的度数与∠AOB有什么关系，并说明理由．
-
科目： 来源： 题型：
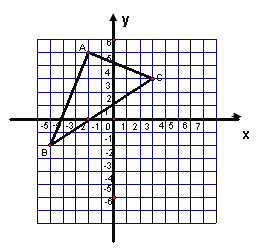
查看答案和解析>>【题目】将△ABC向右平移4个单位长度，再向下平移5个单位长度，
（1）在图上画出对应的三角形A1B1C1；
（2）写出点A1、B1、C1的坐标.
（3）求出△A1B1C1的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”，而把l、4、9、16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的正方形数”都可以看作两个相邻“三角形数”之和．下列等式中。符合这一规律的是( )
A. 15＝4+11 B. 25＝9+16
C. 49＝21+28 D. 61＝25+36
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列语句正确的是( )
A. 1是最小的自然数B. 0没有相反数
C. 绝对值最小的数是0D. 倒数等于它本身的数只有1
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)由四舍五入得到的近似数0.600精确到________位；(2)近似数3.0万精确到________位．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是按一定规律排列的一列数：
第1个数：
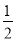—(1+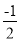
)；第2个数：
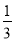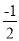—(1+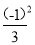 
)(1+
)(1+(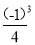
))；第3个数：
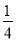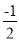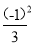－(1+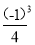
)( 1+
)(1+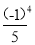
)(1+
)(1+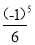
))；第n个数：
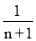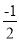－(1+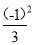 
)(1+
)(1+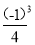
)…(1 +
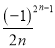)．那么。在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）
A. 第10个数 B. 第11个数 C. 第12个数 D. 第13个数
相关试题
