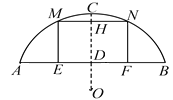
【题目】如图,某菜农在蔬菜基地搭建了一个横截面为圆弧形的蔬菜大棚,大棚的跨度弦AB的长为![]() 米,大棚顶点C离地面的高度为2.3米.
米,大棚顶点C离地面的高度为2.3米.
(1)求该圆弧形所在圆的半径;
(2)若该菜农的身高为1.70米,则他在不弯腰的情况下,横向活动的范围有几米?

参考答案:
【答案】(1)半径为3米;(2)活动范围有3.6米
【解析】试题分析:(1)首先假设半径为xm,再利用勾股定理求出即可;
(2)首先构造直角三角形,进而利用勾股定理得出答案.
试题解析:(1)如图所示:CO⊥AB于点D,
设圆弧形所在圆的半径为xm,根据题意可得:
DO2+BD2=BO2,
则(x-2.3)2+(![]() ×
×![]() )2=x2,
)2=x2,
解得:x=3.

答:圆弧形所在圆的半径为3米;
(2)如图所示:当MN=1.7m,则过点N作NF⊥CO于点F,
可得:DF=1.7m,则FO=2.4m,NO=3m,
故FN=![]() =1.8(m),
=1.8(m),
故该菜农身高1.70m,则他在不弯腰的情况下,横向活动的范围有3.6米.
-
科目: 来源: 题型:
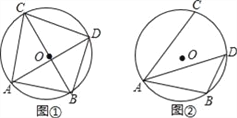
查看答案和解析>>【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在疫情期间的复学准备工作中,为了贯彻落实“生命重于泰山,安全至关重要”的思想,计划购买室内、室外两种型号的消毒液.已知每桶室外消毒液的价格比每桶室内消毒液的价格多30元,买2桶室内消毒液和3桶室外消毒液共需340元.
(1)求室内、室外两种型号消毒液每桶的价格;
(2)根据学校实际情况,需购买室内、室外两种型号的消毒液共200桶,总费用不高于1.4万元,问室内消毒液至少要购买多少桶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的直径为10cm,弦AB∥CD,且AB=8cm,CD=6cm,则弦AB与CD之间的距离为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某地有一座圆弧形的拱桥,桥下水面宽为7.2m,拱顶高出水面2.4m,现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B,C是数轴上三点,点C表示的数为6,BC=4,AB=12.

(1)写出数轴上点A,B表示的数.
(2)动点P,Q分别从A,C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动.若M为AP的中点,点N在线段CQ上,且CN=
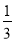 CQ,设运动时间为ts(t>0).
CQ,设运动时间为ts(t>0).①写出数轴上点M,N表示的数(用含t的式子表示).
②t为何值时,原点O恰为线段PQ的中点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,
 表示5与 -2之差的绝对值,实际上也可以理解为 5 与 -2两数在数轴上所对的两点之间的距离,则使得
表示5与 -2之差的绝对值,实际上也可以理解为 5 与 -2两数在数轴上所对的两点之间的距离,则使得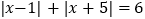 这样的整数
这样的整数 有____个.
有____个.
相关试题

