【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
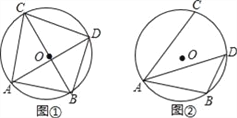
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
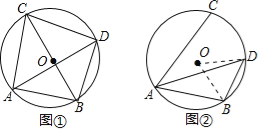
(2)如图②,若∠CAB=60°,求BD的长.
参考答案:
【答案】(Ⅰ)AC =8;BD=CD=5![]() ;(Ⅱ)BD=5.
;(Ⅱ)BD=5.
【解析】试题分析:(1)、根据直径得出∠CAB=∠BDC=90°,然后根据Rt△CAB的勾股定理得出AC的长度,然后根据等腰直角△BDC求出BD和CD的长度;(2)、连接OB,OD,根据AD平分∠CAB,且∠CAB=60°得出∠DOB=2∠DAB=60°,从而得出△OBD为等边三角形,从而得出BD的长度.
试题解析:(1)、如图①,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6, ∴由勾股定理得到:AC=![]() =
=![]() =8.
=8.
∵AD平分∠CAB, ∴![]() =
=![]() ,∴CD=BD.
,∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,∴易求BD=CD=5![]() ;
;
(2)、如图②,连接OB,OD. ∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=![]() ∠CAB=30°,∴∠DOB=2∠DAB=60°.
∠CAB=30°,∴∠DOB=2∠DAB=60°.
又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5, ∴BD=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元;
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,如果收入120元记作+120元,那么﹣100元表示( )
A.支出20元
B.收入20元
C.支出100元
D.收入100元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=-x2+bx+c经过点B(-1,0)和点C(2,3).
(1)求此抛物线的函数表达式;
(2)如果此抛物线上下平移后过点(-2,-1),请直接写出平移的方向和平移的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某住宅小区有一正南朝向的居民楼,如下图,该居民楼的一楼是高6m的小区超市,超市以上是居民住房.在该楼前方15m处准备盖一幢高20m的新楼.已知当地冬季正午的阳光与水平线夹角为32°.
(1)超市以上居民住房采光是否受到影响?为什么?
(2)若要使居民住房采光不受影响,两楼至少应相距多少米?
 (结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)
(结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈) -
科目: 来源: 题型:
查看答案和解析>>【题目】张老师带学生乘车外出郊游,甲车主说:”不论师生,每人8折,"乙车主说:“学生9折,老师免费,“张老师算了一下,不论坐谁的车,费用一样,则张老师带的学生人数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数,中位数分别为( )
A.3.5,3
B.3,4
C.3,3.5
D.4,3
相关试题

