【题目】如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:
①b2>4ac;②ac>0; ③当x>1时,y随x的增大而减小; ④3a+c>0;⑤任意实数m,a+b≥am2+bm.
其中结论正确的序号是( )

A. ①②③ B. ①④⑤ C. ③④⑤ D. ①③⑤
参考答案:
【答案】D
【解析】
①∵抛物线与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2﹣4ac>0,即b2>4ac,故①正确;
②∵开口向下,与y轴的交点在x轴的上方,
∴a<0,c>0,
∴ac<0,故②错误;
③由图象和二次函数图象的对称轴是x=1,可得当x>1时,y随x的增大而减小,
故③正确;
④∵二次函数y=ax2+bx+c过点A (3,0),对称轴是x=1,
∴抛物线与x轴的另一交点坐标为(﹣1,0),﹣![]() =1,即b=﹣2a,
=1,即b=﹣2a,
∴当x=﹣1时,y=0,即a﹣b+c=0,
∴a+2a+c=0,
∴3a+c=0,
故④错误;
⑤∵二次函数图象的对称轴是x=1,且开口向下,
∴当x=1时,y最大,
∴任意实数m,a+b+c≥am2+bm+c.
即任意实数m,a+b≥am2+bm.
故⑤正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
 :
: 与
与 轴相交于B,与
轴相交于B,与 轴相交于点A.直线
轴相交于点A.直线 :
: 经过原点,并且与直线
经过原点,并且与直线 相交于C点.
相交于C点.(1)求ΔOBC的面积;
(2)如图2,在
 轴上有一动点E,连接CE.问CE+
轴上有一动点E,连接CE.问CE+ BE是否有最小值,如果有,求出相应的点E的坐标及CE+
BE是否有最小值,如果有,求出相应的点E的坐标及CE+ BE的最小值;如果没有,请说明理由;
BE的最小值;如果没有,请说明理由;(3)如图3,在(2)的条件下,以CE为一边作等边ΔCDE,D点正好落在
 轴上.将ΔDCE绕点D顺时针旋转,旋转角度为
轴上.将ΔDCE绕点D顺时针旋转,旋转角度为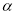 (0°≤
(0°≤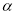 ≤360),记旋转后的三角形为ΔDCE′,点C,E的对称点分别为C′,E′.在旋转过程中,设C′E′所在的直线与直线
≤360),记旋转后的三角形为ΔDCE′,点C,E的对称点分别为C′,E′.在旋转过程中,设C′E′所在的直线与直线 相交于点M,与
相交于点M,与 轴正半轴相交于点N.当ΔOMN为等腰三角形时,求线段ON的长?
轴正半轴相交于点N.当ΔOMN为等腰三角形时,求线段ON的长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在半径为13的圆O中,弦AB平行于弦CD,弦AB和弦CD之间的距离为6,若AB=24,则CD长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=
 (x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.
(x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.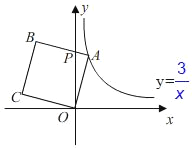
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

相关试题

