【题目】如图所示,△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.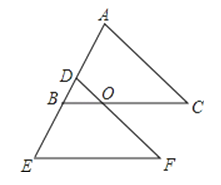
参考答案:
【答案】解:(1)∵△ABC平移后得到△DEF,
∴∠ABC=∠E=60°,
在△ABC中,∠C=180°﹣∠A﹣∠ABC=180°﹣80°﹣60°=40°;
(2)OD=OB.
理由如下:∵AC=BC,
∴∠A=∠ABC,
由平移的性质得,∠A=∠EDF,
∴∠ABC=∠EDF,
∴OD=OB.
【解析】(1)根据平移变换只改变图形的位置不改变图形的形状可得∠ABC=∠E,再根据三角形的内角和等于180°列式计算即可得解;
(2)根据等边对等角可得∠A=∠ABC,再根据平移的性质求出∠A=∠EDF,然后求出∠ABC=∠EDF,最后利用等角对等边解答即可.
【考点精析】关于本题考查的平移的性质,需要了解①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能得出正确答案.
-
科目: 来源: 题型:
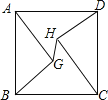
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
A.
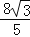 B.2
B.2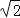 C.
C.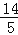 D.10﹣5
D.10﹣5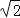
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某小区15户居民今年3月份的用水情况统计表:
月用水量(吨/户)
5
8
12
15
18
居民(户数)
1
2
3
4
5
则今年3月这15户居民用水量的中位数是( )
A.8B.12C.15D.18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为( ).
A.y=x+2
B.y=-x+2
C.y=x+2或y=-x+2
D.y=-x+2或y=x-2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,有一个锐角是另一个锐角的4倍,求这个直角三角形各个角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△ABC的两边长分别为3和5,那么连结△ABC三边中点D、E、F所得的△DEF的周长可能是( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn的面积为Sn,则Sn= .(用含n的式子表示)

相关试题

