【题目】在正方形![]() 中,点
中,点![]() 是直线
是直线![]() 上一点.连接
上一点.连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .
.
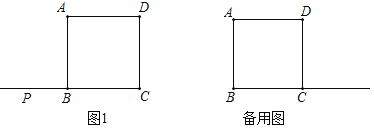
(1)如图1.若点![]() 在线段
在线段![]() 的延长线上过点
的延长线上过点![]() 作
作![]() 于
于![]() .与对角线
.与对角线![]() 交于点
交于点![]() .
.
①请仔细阅读题目,根据题意在图上补全图形;②求证:![]() .
.
(2)若点![]() 在射线
在射线![]() 上,直接写出
上,直接写出![]() ,
,![]() ,
,![]() 三条线段之间的数量关系(不必写过程).
三条线段之间的数量关系(不必写过程).
参考答案:
【答案】(1)①见解析;②见解析;(2)EC=![]() (CD-PC)或EC=
(CD-PC)或EC=![]() (CD+PC)
(CD+PC)
【解析】
(1)①构建题意画出图形即可;②想办法证明△APB≌△PEH即可;
(2)结论:当点P在线段BC上时:![]() .当点P在线段BC的延长线上时:
.当点P在线段BC的延长线上时:![]() ,构造全等三角形即可解决问题.
,构造全等三角形即可解决问题.
解:(1)①补全图形如图所示.
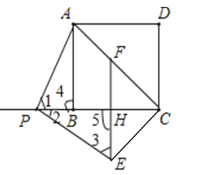
②证明:![]() 线段
线段![]() 绕点
绕点![]() 顺时针能转
顺时针能转![]() 得到线段
得到线段![]() ,
,
![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
![]()
![]()
![]() 于
于![]() ,
,
![]()
![]()
![]()
![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
∴![]() ;
;
(2)当点P在线段BC上时:![]() .
.
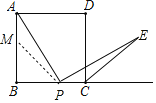
理由:在BA上截取BM=BP.则△PBM是等腰直角三角形,PM=![]() PB.
PB.
易证△PCE≌△AMP,可得EC=PM,
∵CD-PC=BC-PC=PB,
∴EC=PM=![]() PB=
PB=![]() (CD-PC),
(CD-PC),
当点P在线段BC的延长线上时:![]() .
.
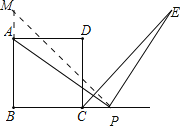
理由:在BA上截取BM=BP.则△PBM是等腰直角三角形,PM=![]() PB.
PB.
易证△PCE≌△AMP,可得EC=PM,
∵CD+PC=BC+PC=PB,
∴EC=PM=![]() PB=
PB=![]() (CD+PC).
(CD+PC).
故答案为EC=![]() (CD-PC)或EC=
(CD-PC)或EC=![]() (CD+PC).
(CD+PC).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,是由一些棱长为单位1的相同的小正方体组合成的简单几何体.
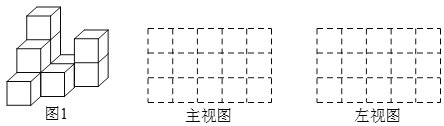
(1)图中有 个小正方体;
(2)请在图1右侧方格中分别画出几何体的主视图、左视图;
(3)不改变(2)中所画的主视图和左视图,最多还能在图1中添加 个小正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,同学们的学习习惯也有了改变,一些同学在做题遇到困难时,喜欢上网查找答案.针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图.
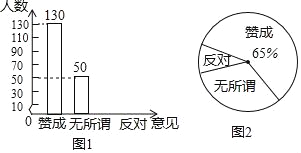
请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名学生?
(2)将图1补充完整;
(3)求出扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校1500名学生中有多少名学生持“无所谓”意见.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的顶点A、D分别落在x轴、y轴,OD=2OA=6,AD:AB=3:1.则点B的坐标是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
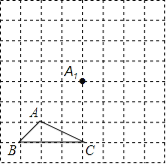
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.

(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
相关试题

