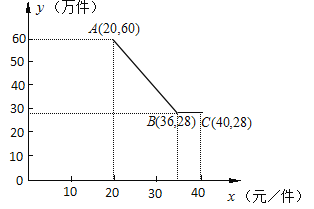
【题目】华宇公司获得授权生产某种奥运纪念品,经市场调查分析,该纪念品的销售量![]() (万件)与纪念品的价格
(万件)与纪念品的价格![]() (元/件)之间的函数图象如图所示,该公司纪念品的生产数量
(元/件)之间的函数图象如图所示,该公司纪念品的生产数量![]() (万件)与纪念品的价格
(万件)与纪念品的价格![]() (元/件)近似满足函数关系式
(元/件)近似满足函数关系式 ![]() ,若每件纪念品的价格不小于20元,且不大于40元.
,若每件纪念品的价格不小于20元,且不大于40元.
请解答下列问题:
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当价格![]() 为何值时,使得纪念品产销平衡(生产量与销售量相等);
为何值时,使得纪念品产销平衡(生产量与销售量相等);
![]() (3)当生产量低于销售量时,政府常通过向公司补贴纪念品的价格差来提高生产量,促成新的产销平衡.若要使新的产销平衡时销售量达到46万件,政府应对该纪念品每件补贴多少元?
(3)当生产量低于销售量时,政府常通过向公司补贴纪念品的价格差来提高生产量,促成新的产销平衡.若要使新的产销平衡时销售量达到46万件,政府应对该纪念品每件补贴多少元?
参考答案:
【答案】(1)、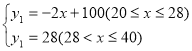 ;(2)、30元或38元;(3)、1元.
;(2)、30元或38元;(3)、1元.
【解析】
试题分析:(1)、首先设出函数解析式,然后利用待定系数法求出函数解析式,本题需要注意的是分段函数;(2)、根据题意分两种情况列出二元一次方程组,然后进行求解;(3)、分别根据两个函数值等于46求出对应的x的值,然后进行做差得出答案.
试题解析:(1)、设![]() 与
与![]() 的函数解析式为:
的函数解析式为:![]() ,将点
,将点![]() 、
、![]() 代入
代入![]() 得:
得:
![]() 解得:
解得:![]()
∴![]() 与
与![]() 的函数关系式为:
的函数关系式为: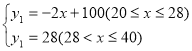
、当![]() 时,有
时,有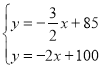 解得:
解得:![]()
当![]() 时,有
时,有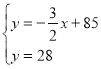 解得:
解得:![]()
∴当价格为30元或38元,可使公司产销平衡
(3)、当![]() 时,则
时,则![]() ,∴
,∴![]()
当![]() 时,则
时,则![]() ,∴
,∴![]() ∴
∴![]()
![]()
∴政府对每件纪念品应补贴1元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙O的圆心在坐标原点,半径为3.过A(-7,9),B(0,9)的抛物线
 (a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD. 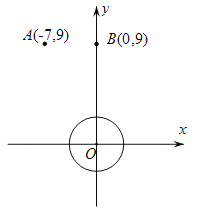
(1)若点D的坐标为D(3,0).①请直接写出此时直线AD与⊙O的位置关系;②求此时抛物线对应的函数关系式;
(2)若直线AD和⊙O相切,求抛物线二次项系数a的值;
(3)当直线AD和⊙O相交时,直接写出a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3xa+1y2b与﹣4x2y8﹣a是同类项,则a﹣2b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=ax2+bx+c与x轴交于点A(0,4)、E(0,-2)两点,与y轴交于点B(2,0),连结AB。过点A作直线AK⊥AB,动点P从点A出发以每秒
 个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处。
个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处。
(1)、求抛物线的解析式;
(2)、当点D在△ABP的内部时,△ABP与△ADP不重叠部分的面积为S,求S与t之间的函数关系式,并直接写出t的取值范围;
(3)、是否存在这样的时刻,使动点D到点O的距离最小,若存在请求出这个最小距离,若不存在说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市同价销售同一款可拆分式驱蚊器,1套驱蚊器由1个加热器和1瓶电热蚊香液组成.电热蚊香液作为易耗品可单独购买,1瓶电热蚊香液的售价是1套驱蚊器的
 .已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
.已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.(1)求1套驱蚊器和1瓶电热蚊香液的售价;
(2)为了促进该款驱蚊器的销售,甲超市打8.5折销售,而乙超市采用的销售方法是顾客每买1套驱蚊器送1瓶电热蚊香液.在这段促销期间,甲超市销售2000套驱蚊器,而乙超市在驱蚊器销售上获得的利润不低于甲超市的1.2倍.问乙超市至少销售多少套驱蚊器?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.平行四边形的对角线互相平分且相等B.矩形的对角线相等且互相平分
C.菱形的对角线互相垂直且相等D.正方形的对称轴是正方形的对角线
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=a(x-h)2+k(a≠0)的顶点坐标是______,对称轴是______,当x=______时,y有最值______;当a>0时,若x______时,y随x增大而减小.
相关试题

