【题目】如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( ) 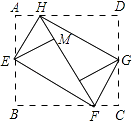
A.12cm
B.16cm
C.20cm
D.28cm
参考答案:
【答案】C
【解析】解:∵∠HEM=∠AEH,∠BEF=∠FEM, ∴∠HEF=∠HEM+∠FEM= ![]() ×180°=90°,
×180°=90°,
同理可得:∠EHG=∠HGF=90°,
∴四边形EFGH为矩形.
∴EH=FG,EH∥FG,
∴∠EHF=∠HFG,
∵∠AHE=∠EHF,∠CFG=∠HFG,
∴∠AHE=∠CFG,
∵∠A=∠C,
∴△AHE≌△CFG,
∴AH=CF,
∴AH=CF=FP,
∵HD=HP,
∴AD=AH+HD=PF+HP=HF,
∵HF= ![]() =
= ![]() =20,
=20,
∴AD=20cm,
故选C.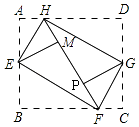
利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,那么由折叠可得HF的长即为边AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将三角形各顶点的纵坐标都减去5,横坐标保持不变,所得图形与原图形相比( )
A. 向上平移了5个单位B. 向下平移了5个单位
C. 向左平移了5个单位D. 向右平移了5个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
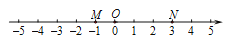
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3a2b+6ab2=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的边数由原来的3增加到n时(n>3,且n为正整数),它的外角和( )
A. 增加(n﹣2)×180° B. 减小(n﹣2)×180° C. 增加(n﹣1)×180° D. 没有改变
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是方程x2﹣4mx+m2=0的一个根,代数式m(m﹣8)﹣1的值为_____.
相关试题

