Question

【题目】填写下面证明过程中的推理依据：

已知：如图，AB∥CD，BE平分∠ABC，CF平分∠BCD．求证：∠1=∠2

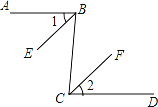
证明：∵AB∥CD （__________）

∴∠ABC=∠BCD（__________）

∵BE平分∠ABC，CF平分∠BCD （__________）

∴∠1=∠ ______ ，（__________）

∠2=∠ ______ ．（__________）

∴∠1=∠2．（__________）

Answer 1

【答案】已知；两直线平行，内错角相等；已知；ABC；角平分线的定义；BCD；角平分线的定义；等量代换．

【解析】试题分析：先根据平行线的性质，得出∠ABC=∠BCD，再根据角平分线的定义，即可得出∠1=∠2．

试题解析：证明：∵AB∥CD(已知)

∴∠ABC=∠BCD(两直线平行,内错角相等)

∵BE平分∠ABC,CF平分∠BCD(已知)

∴∠1=∠ABC,(角平分线的定义)

∠2=∠BCD.(角平分线的定义)

∴∠1=∠2.(等量代换)

故答案为：已知；两直线平行，内错角相等；已知；ABC；角平分线的定义；BCD；角平分线的定义；等量代换