【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.

参考答案:
【答案】(1)y=![]() x2+
x2+![]() x;(2)①P点坐标为P1(
x;(2)①P点坐标为P1(![]() ,-
,-![]() )或P2(
)或P2(![]() ,﹣
,﹣![]() )或P3(
)或P3(![]() ,﹣
,﹣![]() ),②D(
),②D(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)首先解方程得出A,B两点的坐标,进而利用待定系数法求出二次函数解析式即可;
(2)①首先求出AB的直线解析式,以及BO解析式,再利用等腰三角形的性质得出当OC=OP时,当OP=PC时,点P在线段OC的中垂线上,当OC=PC时分别求出x的值即可;
②利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数,进而得出最值即可.
试题解析:解(1)解方程x2﹣2x﹣3=0,
得 x1=3,x2=﹣1.
∵m<n,
∴m=﹣1,n=3
∴A(﹣1,﹣1),B(3,﹣3).
∵抛物线过原点,设抛物线的解析式为y=ax2+bx(a≠0).
∴![]() ,
,
解得: 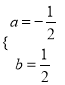 ,
,
∴抛物线的解析式为y=![]() x2+
x2+![]() x .
x .
(2)①设直线AB的解析式为y=kx+b.
∴![]() ;解得:
;解得: 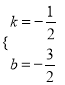 ,
,
∴直线AB的解析式为y=![]() x+
x+![]() .
.
∴C点坐标为(0,-![]() ).
).
∵直线OB过点O(0,0),B(3,﹣3),
∴直线OB的解析式为y=﹣x.
∵△OPC为等腰三角形,
∴OC=OP或OP=PC或OC=PC.
设P(x,﹣x),
(i)当OC=OP时,x2+(-x)2=![]() .
.
解得x1=![]() ,x2=-
,x2=-![]() ,(舍去).
,(舍去).
∴P1(![]() ,-
,-![]() ).
).
(ii)当OP=PC时,点P在线段OC的中垂线上,
∴P2(![]() ,﹣
,﹣![]() ).
).
(iii)当OC=PC时,由x2+(-x+![]() )2=
)2=![]() ,
,
解得x1=![]() ,x2=0(舍去).
,x2=0(舍去).
∴P3(![]() ,﹣
,﹣![]() ).
).
∴P点坐标为P1(![]() ,-
,-![]() )或P2(
)或P2(![]() ,﹣
,﹣![]() )或P3(
)或P3(![]() ,﹣
,﹣![]() ).
).
②过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
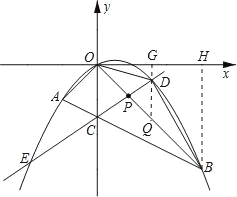
设Q(x,﹣x),D(x,-![]() x2+
x2+![]() x).
x).
S△BOD=S△ODQ+S△BDQ=![]() DQOG+
DQOG+![]() DQGH,
DQGH,
=![]() DQ(OG+GH),
DQ(OG+GH),
=![]() [x+(
[x+(![]() +
+ ![]() )]×3,
)]×3,
=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∵0<x<3,
∴当x=![]() 时,S取得最大值为
时,S取得最大值为![]() ,此时D(
,此时D(![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两工程队合作完成一项工程,需要12天完成,工程费用共36000元,若甲、乙两工程队单独完成此项工程,乙工程队所用的时间是甲工程队的1.5倍,乙工程队每天的费用比甲工程队少800元.
(1)问甲、乙两工程队单独完成此项工程各需多少天?
(2)若让一个工程队单独完成这项工程,哪个工程队的费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=
 ,AB=3,求BD的长.
,AB=3,求BD的长.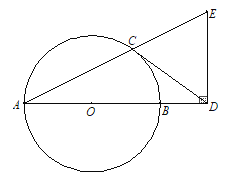
-
科目: 来源: 题型:
查看答案和解析>>【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台)
售价(元/台)
电饭煲
200
250
电压锅
160
200
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的
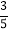 ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少? -
科目: 来源: 题型:
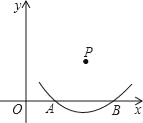
查看答案和解析>>【题目】如图,在直角坐标系中,以点P为圆心的圆弧与x轴交于A、B两点,已知P(4,2)和A(2,0),则点B的坐标是_____.
相关试题

