【题目】如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为 ![]() 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 .
的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 . 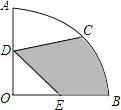
参考答案:
【答案】( ![]() π+
π+ ![]() ﹣
﹣ ![]() )
)
【解析】解:连结OC,过C点作CF⊥OA于F,
∵半径OA=2cm,C为 ![]() 的中点,D、E分别是OA、OB的中点,
的中点,D、E分别是OA、OB的中点,
∴OD=OE=1cm,OC=2cm,∠AOC=45°,
∴CF= ![]() ,
,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积
= ![]() ﹣
﹣ ![]() ×
× ![]()
= ![]() π﹣
π﹣ ![]() (cm2)
(cm2)
三角形ODE的面积= ![]() OD×OE=
OD×OE= ![]() (cm2),
(cm2),
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积
= ![]() ﹣(
﹣( ![]() π﹣
π﹣ ![]() )﹣
)﹣ ![]()
= ![]() π+
π+ ![]() ﹣
﹣ ![]() (cm2).
(cm2).
故图中阴影部分的面积为( ![]() π+
π+ ![]() ﹣
﹣ ![]() )cm2 .
)cm2 .
所以答案是:( ![]() π+
π+ ![]() ﹣
﹣ ![]() ).
).
【考点精析】掌握扇形面积计算公式是解答本题的根本,需要知道在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )

A. 点F B. 点E C. 点A D. 点C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3
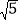 ,且∠ECF=45°,则CF长为( )
,且∠ECF=45°,则CF长为( )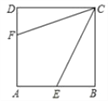
A. 2
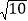 B. 3
B. 3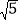 C.
C. 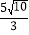 D.
D. 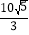
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N.求证:△ABN≌△CDM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C比∠AED小55°,则∠AED的度数为( )
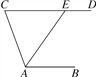
A. 55° B. 125° C. 135° D. 140°
相关试题

