【题目】如图,已知∠1,∠2互为补角,且∠3=∠B, 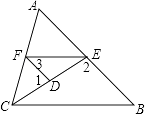
(1)求证:∠AFE=∠ACB;
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
参考答案:
【答案】
(1)证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=80°,∠3=45°,
∴∠FED=80°﹣45°=35°,
∵EF∥BC,
∴∠BCE=∠FED=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∴∠AFE=∠ACB=70°.
【解析】(1)求出DF∥AB,推出∠3=∠AEF,求出∠B=∠AEF,得出FE∥BC,根据平行线性质求出即可;(2)求出∠FED=80°﹣45°=35°,根据平行线性质求出∠BCE=∠FED=35°,求出∠ACB=2∠BCE=70°,根据平行线性质求出即可.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过A(-2, 0), C(0, 6)两点的抛物线y=-
 x2+ax+b与x轴交于另一点B,点D是抛物线的顶点.
x2+ax+b与x轴交于另一点B,点D是抛物线的顶点.(1)求a、b的值;
(2)点P是x轴上的一个动点,过P作直线l//AC交抛物线于点Q.随着点P的运动,若以A、P、Q、C为顶点的四边形是平行四边形,请直接写出符合条件的点Q的坐标;
(3)在直线AC上是否存在一点M,使△BDM的周长最小,若存在,请找出点M并求出点M的坐标.若不存在,请说明理由。


备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB与∠BOC互为邻补角,且∠BOC>∠AOB.OD平分∠AOB,射线OE使∠BOE=
 ∠EOC,当∠DOE=72°时,则∠EOC的度数为 .
∠EOC,当∠DOE=72°时,则∠EOC的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程: 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
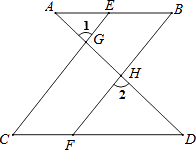
∵∠1=∠2(已知),
且∠1=∠CGD(),
∴∠2=∠CGD(等量代换).
∴CE∥BF().
∴∠=∠C().
又∵∠B=∠C(已知),
∴∠=∠B(等量代换).
∴AB∥CD(). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系中,已知点A(0,2)、点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
(1)填空:点D的坐标为_________,点E的坐标为_______________.
(2)若抛物线
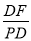 经过A、D、E三点,求该抛物线的解析式.
经过A、D、E三点,求该抛物线的解析式.(3)若正方形和抛物线均以每秒
 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在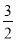 轴上时,正方形和抛物线均停止运动.
轴上时,正方形和抛物线均停止运动. ①在运动过程中,设正方形落在y轴右侧部分的面积为
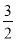 ,求
,求 关于平移时间
关于平移时间 (秒)的函数关系式,并写出相应自变量
(秒)的函数关系式,并写出相应自变量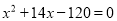 的取值范围.
的取值范围.②运动停止时,求抛物线的顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的一个外角为30°,那么这个正多边形的边数是( )
A.6
B.11
C.12
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式加上2x2﹣4x﹣3得﹣x2﹣3x,则这个多项式为 .
相关试题

