搜索
【题目】已知∠AOB与∠BOC互为邻补角，且∠BOC＞∠AOB．OD平分∠AOB，射线OE使∠BOE= 
∠EOC，当∠DOE=72°时，则∠EOC的度数为 ．
参考答案：
【答案】72°
【解析】解：如图1 
，
设∠AOD=∠DOB=x°，∠BOE=y°，则∠EOC=2y°．
根据题意，x+y=72，
∵2x+3y=2x+2y+y=2（x+y）+y=180，
∴2×72+y=180，
∴y=180﹣144=36，
∴∠EOC=36°×2=72°．
所以答案是：72°．
【考点精析】利用角的平分线和对顶角和邻补角对题目进行判断即可得到答案，需要熟知从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知y＝0是关于y的一元二次方程（m﹣1）y2+my+4m2﹣4＝0的一个根，那么m的值是（ ）
A. 0B. ±1C. 1D. ﹣1
-
科目： 来源： 题型：
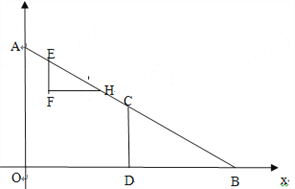
查看答案和解析>>【题目】如图，在直角坐标系中，点A(0，6)，B(8，0)，点C是线段AB的中点，CD⊥OB交OB于D，Rt△EFH的斜边EH在射线AB上，顶点F在射线AB的左侧，EF∥OA，点E从点A出发，以每秒1个单位的速度向B运动，到点B停止，AE=EF，运动时间为t（s）.
（1）在Rt△EFH中，EF= ，EH= ,点F坐标为（ ， ）（用含t的代数式表示）
（2）t为何值时，H与C重合？
（3）设△EFH与△CDB重叠部分图形的面积为S(S>0)，求S与t的函数关系式。
（4）在整个运动过程中，Rt△EFH扫过的面积是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，过A(－2, 0), C(0, 6)两点的抛物线y＝－
x2＋ax＋b与x轴交于另一点B，点D是抛物线的顶点．（1）求a、b的值；
（2）点P是x轴上的一个动点，过P作直线l//AC交抛物线于点Q．随着点P的运动，若以A、P、Q、C为顶点的四边形是平行四边形，请直接写出符合条件的点Q的坐标；
(3)在直线AC上是否存在一点M，使△BDM的周长最小，若存在，请找出点M并求出点M的坐标．若不存在，请说明理由。
备用图
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面推理过程： 如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：
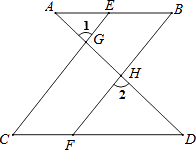
∵∠1=∠2（已知），
且∠1=∠CGD（），
∴∠2=∠CGD（等量代换）．
∴CE∥BF（）．
∴∠=∠C（）．
又∵∠B=∠C（已知），
∴∠=∠B（等量代换）．
∴AB∥CD（）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1，∠2互为补角，且∠3=∠B，
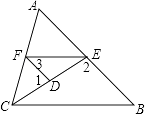
（1）求证：∠AFE=∠ACB；
（2）若CE平分∠ACB，且∠1=80°，∠3=45°，求∠AFE的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在直角坐标系中，已知点A（0，2）、点B（-2，0），过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE.
（1）填空：点D的坐标为_________，点E的坐标为_______________.
（2）若抛物线
经过A、D、E三点，求该抛物线的解析式.（3）若正方形和抛物线均以每秒
个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在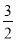
轴上时，正方形和抛物线均停止运动. ①在运动过程中，设正方形落在y轴右侧部分的面积为
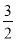，求
关于平移时间
（秒）的函数关系式，并写出相应自变量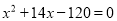
的取值范围.②运动停止时，求抛物线的顶点坐标.
相关试题
