搜索
【题目】如果一个正多边形的一个外角为30°，那么这个正多边形的边数是（ ）
A.6
B.11
C.12
D.18
参考答案：
【答案】C
【解析】解：这个正多边形的边数：360°÷30°=12，
故选C．
【考点精析】解答此题的关键在于理解多边形内角与外角的相关知识，掌握多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面推理过程： 如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：
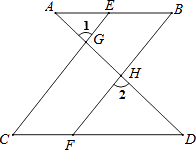
∵∠1=∠2（已知），
且∠1=∠CGD（），
∴∠2=∠CGD（等量代换）．
∴CE∥BF（）．
∴∠=∠C（）．
又∵∠B=∠C（已知），
∴∠=∠B（等量代换）．
∴AB∥CD（）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1，∠2互为补角，且∠3=∠B，
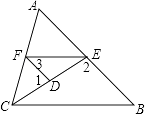
（1）求证：∠AFE=∠ACB；
（2）若CE平分∠ACB，且∠1=80°，∠3=45°，求∠AFE的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在直角坐标系中，已知点A（0，2）、点B（-2，0），过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE.
（1）填空：点D的坐标为_________，点E的坐标为_______________.
（2）若抛物线
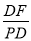经过A、D、E三点，求该抛物线的解析式.（3）若正方形和抛物线均以每秒
个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在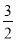
轴上时，正方形和抛物线均停止运动. ①在运动过程中，设正方形落在y轴右侧部分的面积为
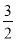，求
关于平移时间
（秒）的函数关系式，并写出相应自变量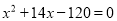
的取值范围.②运动停止时，求抛物线的顶点坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个多项式加上2x2﹣4x﹣3得﹣x2﹣3x，则这个多项式为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°
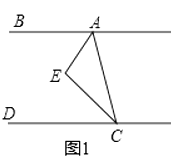
（1）请判断AB与CD的位置关系并说明理由；
（2）如图2，在（1）的结论下，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？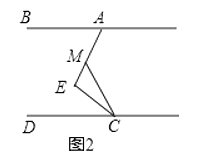
（3）如图3，在（1）的结论下，P为线段AC上一定点，点Q为直线CD上一动点，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？ （2、3小题只需选一题说明理由）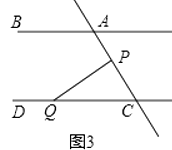
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据要求计算：
（1）计算：|
﹣ 
|+ 
+ 
（2）解方程组： ①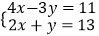
②
．
相关试题
