【题目】某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程 (千米)与时间 (分)关系的图象,根据图象信息,下列说法正确的是 ( )
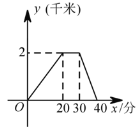
A. 小王去时的速度大于回家的速度 B. 小王去时走上坡路,回家时走下坡路
C. 小王去时所花时间少于回家所花时间 D. 小王在朋友家停留了 ![]() 分
分
参考答案:
【答案】D
【解析】A、根据速度=路程÷时间,可求出小王去时的速度和回家的速度,比较后可得出A不正确;B、题干中未给出路况如何,故B不正确;C、先求出小王回家所用时间,比较后可得出C不正确;D、观察函数图象,求出小王在朋友家停留的时间,故D正确.综上即可得出结论.
A、小王去时的速度为2000÷20=100(米/分),
小王回家的速度为2000÷(40-30)=200(米/分),
∵100<200,
∴小王去时的速度小于回家的速度,A不正确;
B、∵题干中未给出小王去朋友家的路有坡度,
∴B不正确;
C、40-30=10(分),
∵20>10,
∴小王去时所花时间多于回家所花时间,C不正确;
D、∵30-20=10(分),
∴小王在朋友家停留了10分,D正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图B,E,C,F, 四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断 △ABC≌△DEF 的是 ( )
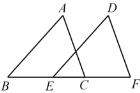
A. ∠A=∠D B. DF∥AC C. AC=DF D. AB=DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(﹣1,4).
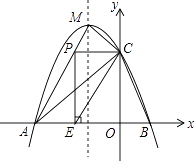
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD与△ACB面积相等时,求点D的坐标;
(3)点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将△PCE沿直线CE翻折,使点P的对应点P′与P、E、C处在同一平面内,请求出点P′坐标,并判断点P′是否在该抛物线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以菱形ABCD对角线交点为坐标原点,建立平面直角坐标系,A、B两点的坐标分别为(﹣2
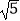 ,0)、(0,﹣
,0)、(0,﹣ 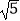 ),直线DE⊥DC交AC于E,动点P从点A出发,以每秒2个单位的速度沿着A→D→C的路线向终点C匀速运动,设△PDE的面积为S(S≠0),点P的运动时间为t秒.
),直线DE⊥DC交AC于E,动点P从点A出发,以每秒2个单位的速度沿着A→D→C的路线向终点C匀速运动,设△PDE的面积为S(S≠0),点P的运动时间为t秒.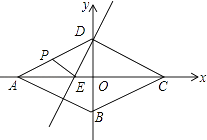
(1)求直线DE的解析式;
(2)求S与t之间的函数关系式,并写出自变量t的取值范围;
(3)当t为何值时,∠EPD+∠DCB=90°?并求出此时直线BP与直线AC所夹锐角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=AC,AB 的垂直平分线交 AB 于点 D,交 CA 的延长线于点 E,∠EBC=42°,则 ∠BAC=( )

A. 159° B. 154° C. 152° D. 138°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一项工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款1.5万元,乙工程队工程款1.1万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用5天;
(3)若甲、乙两队合作4天,余下的工程由乙队单独也正好如期完成.
在不耽误工期的情况下,你觉得那一种施工方案最节省工程款?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成
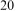 个扇形,如图)并规定:顾客在本商场每消费
个扇形,如图)并规定:顾客在本商场每消费  元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 100 元、 50 元、 20 元的购物券.某顾客消费 210 元,他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?
元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 100 元、 50 元、 20 元的购物券.某顾客消费 210 元,他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?
相关试题

