【题目】某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:

(1)机动车行驶几小时后加油?加了多少油?
(2)请求出加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
参考答案:
【答案】(1)5小时, 24L;(2)Q=42-6t;(3)见解析.
【解析】
(1)根据函数图象的横坐标,可得答案;根据函数图象的纵坐标,可得加油量;
(2)根据待定系数法,可得函数解析式;
(3)根据单位耗油量乘以行驶时间,可得行驶路程,根据有理数的大小比较,可得答案.
解:(1)由横坐标看出,5小时后加油,由纵坐标看出,加了36-12=24(L)油;
(2)设解析式为Q=kt+b,将(0,42),(5,12)代入函数解析式,
得![]() ,
,
解得![]() ,
,
故函数解析式为Q=42-6t(0≤t≤5);
(3)够用,理由如下
单位耗油量为![]() =6 L/h,
=6 L/h,
∴6×40-230=240-230=10>0,
还可以再行驶10千米,
故油够用.
-
科目: 来源: 题型:
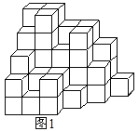
查看答案和解析>>【题目】如图1,是一个由53个大小相同的小正方体堆成的立体图形,从正面观察这个立体图形得到的平面图形如图2所示.
(1)请在图3、图4中依次画出从左面、上面观察这个立体图形得到的平面图形
(2)保持这个立体图形中最底层的小正方体不动,从其余部分中取走k个小正方体,得到一个新的立体图形.如果依次从正面、左面、上面观察新的立体图形,所得到的平面图形分别与图2、图3、图4是一样的,那么k的最大值为 .



-
科目: 来源: 题型:
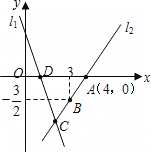
查看答案和解析>>【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的
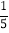 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台? -
科目: 来源: 题型:
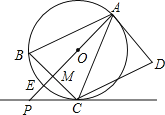
查看答案和解析>>【题目】如图,AD是
 的切线,切点为A,AB是
的切线,切点为A,AB是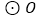 的弦,过点B作
的弦,过点B作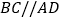 ,交
,交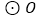 于点C,连接AC,过点C作
于点C,连接AC,过点C作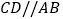 ,交AD于点D,连接AO并延长AO交BC于点M,交
,交AD于点D,连接AO并延长AO交BC于点M,交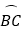 于点E,交过点C的直线于点P,且
于点E,交过点C的直线于点P,且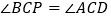 .
.
 求证:
求证: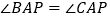 ;
;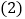 判断直线PC与
判断直线PC与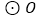 的位置关系,并说明理由;
的位置关系,并说明理由;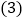 若
若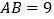 ,
,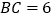 ,求PC的长.
,求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )

A. 75°B. 60°C. 55°D. 45°
相关试题

