搜索
【题目】如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（ ）
A. 75°B. 60°C. 55°D. 45°
参考答案：
【答案】B
【解析】
由正方形的性质和等边三角形的性质得出∠BAE＝150°，AB＝AE，由等腰三角形的性质和内角和定理得出∠ABE＝∠AEB＝15°，再运用三角形的外角性质即可得出结果．
解：∵四边形ABCD是正方形，
∴∠BAD＝90°，AB＝AD，∠BAF＝45°，
∵△ADE是等边三角形，
∴∠DAE＝60°，AD＝AE，
∴∠BAE＝90°+60°＝150°，AB＝AE，
∴∠ABE＝∠AEB＝
（180°﹣150°）＝15°，
∴∠BFC＝∠BAF+∠ABE＝45°+15°＝60°；
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某机动车出发前油箱内有油42L，行驶若干小时后，在途中加油站加油若干升．油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据如图回答问题：
（1）机动车行驶几小时后加油？加了多少油？
（2）请求出加油前油箱余油量Q与行驶时间t之间的关系式；
（3）如果加油站离目的地还有230km，车速为40km/h，要到达目的地，油箱中的油是否够用？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD是
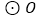的切线，切点为A，AB是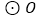的弦，过点B作
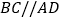，交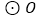于点C，连接AC，过点C作
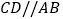，交AD于点D，连接AO并延长AO交BC于点M，交
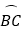于点E，交过点C的直线于点P，且
．
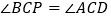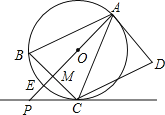
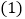求证：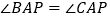
；
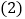判断直线PC与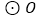的位置关系，并说明理由；
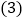若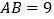
，
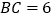，求PC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B，直角顶点P在射线AC上移动，另一边交DC于点Q.
(1)如图①，当点Q在DC边上时，猜想并写出PB与PQ所满足的数量关系，并加以证明；
(2)如图②，当点Q落在DC的延长线上时，猜想并写出PB与PQ满足的数量关系，并证明你的猜想．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线
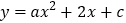与y轴交于点
，与x轴交于点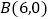
，点P是线段AB上方抛物线上的一个动点．
求这条抛物线的表达式及其顶点坐标；
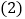当点P移动到抛物线的什么位置时，使得
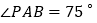，求出此时点P的坐标；
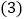当点P从A点出发沿线段AB上方的抛物线向终点B移动，在移动中，点P的横坐标以每秒1个单位长度的速度变动；与此同时点M以每秒1个单位长度的速度沿AO向终点O移动，点P，M移动到各自终点时停止
当两个动点移动t秒时，求四边形PAMB的面积S关于t的函数表达式，并求t为何值时，S有最大值，最大值是多少？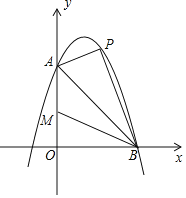
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数a、b、c在数轴上的位置如图所示
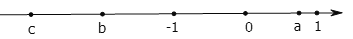
（1）比较a、b、|c|的大小（用“＞”连接）；
（2）若n=|b+c|﹣|c﹣1|﹣|b﹣a|，求
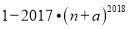的值； （3）若a=
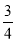，b=﹣2，c=﹣3，且a、b、c对应的点分别为A、B、C，问在数轴上是否存在一点M，使M与B的距离是M与A的距离的3倍，若存在，请求出M点对应的有理数；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】在市举办的“划龙舟，庆端午”比赛中，甲、乙两队在比赛时的路程
（米）与时间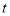
（分钟）之间的函数关系图象如图所示，根据图象得到下列结论，你认为正确的结论是（ ）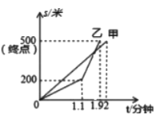
①这次比赛的全程是
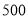米；②乙队先到达终点；③比赛中两队从出发到
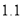分钟时间段，乙队的速度比甲队的速度快；④乙与甲相遇时乙的速度是
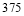米/分钟；⑤在
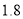分钟时，乙队追上了甲队.A.①③④B.①②⑤C.①②④D.①②③④⑤
相关试题
