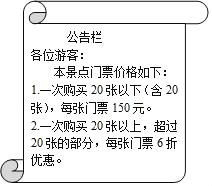
【题目】2018年国庆期间,一旅游团到安徽境内某旅游景点,看到售票处旁边的公告栏如图所示,请根据公告栏内容解答下列问题:(答案直接写在横线上)
(1)若旅游团人数为18人,门票费用是 元;若旅游团人数为22人,门票费用为 _______元.
(2)设旅游团人数为x人,试用含量x的代数式表示该旅游团门票费用y元.
(解)y=![]()
参考答案:
【答案】(1)2700,3180;(2)![]() .
.
【解析】
(1)18人时,根据门票费用=单价×人数列式计算即可得解;22人时,分两个部分,20人按照原价,超过20的人数安装6折计算,然后列出算式进行计算即可得解;
(2)分两段根据门票费用=单价×人数,列式整理即可得解.
(1)150×18=2700(元),
150×20+150×60%×(22﹣20)
=3000+180
=3180(元).
∴若旅游团人数为18人,门票费用是2700元;若人数为22人,门票费用是3180元;
故答案为:2700,3180.
(2)x≤20时,y=150x,
x>10时,y=150×20+150×60%×(x﹣20)
=3000+90x﹣1800
=90x+1200,
∴y=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:|a|=3,b2=4,ab<0,求a﹣b的值.
(2)已知关于x的方程
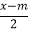 =
=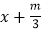 与方程
与方程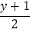 =3y﹣2的解互为倒数,求m的值.
=3y﹣2的解互为倒数,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系为: ;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)求△AEF周长的最小值。
(4) 如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
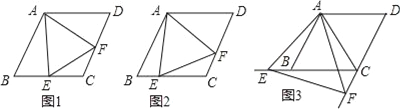
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(3-k)x-2k2+18.
(1)当k为何值时,它的图象经过原点?
(2)当k为何值时,它的图象经过点(0,-2)?
(3)当k为何值时,它的图象平行于直线y=-x?
(4)当k为何值时,y随x增大而减小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上,A、B两点表示的数a,b满足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M从A点向负半轴运动、小球N从B点向正半轴运动,两球同时出发,小球M运动的速度为每秒2个单位,当M运动到OB的中点时,N点也同时运动到OA的中点,则小球N的速度是每秒 个单位;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过 秒后两个小球相距两个单位长度.

相关试题

