【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4).
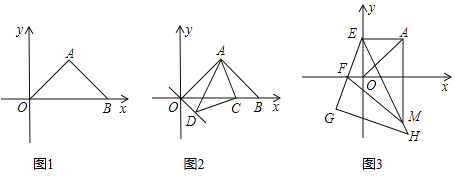
(1)点B坐标为
(2)如图2,若C为x轴正半轴上一动点,以AC为直角边作等腰Rt△ACD,∠ACD=90,连OD,求∠AOD的度数;
(3)如图3,过点A作y轴的垂线交y轴于点E,F为x轴负半轴上一点,点G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过点A作x轴垂线交EH于点M,连FM,等式![]() =1是否成立?若成立,请证明;若不成立,说明理由.
=1是否成立?若成立,请证明;若不成立,说明理由.
参考答案:
【答案】(1)(8,0);(2)90°;(3)![]() =1成立,理由详见解析.
=1成立,理由详见解析.
【解析】
(1)因为△AOB为等腰直角三角形,A(4,4),作AE⊥OB于E,则B点坐标可求;(2)作AE⊥OB于E,DF⊥OB于F,求证△DFC≌△CEA,再根据等量变换,证明△AOB为等腰直角三角形,则∠AOD的度数可求;(3)等式成立.在AM上截取AN=OF,连EN,易证△EAN≌△EOF,再根据角与角之间的关系,证明△NEM≌△FEM,则有AM-MF=OF,即可求证等式成立.
(1)作AE⊥OB于E,

∵A(4,4),
∴OE=4,
∵△AOB为等腰直角三角形,且AE⊥OB,
∴OE=EB=4,
∴OB=8,
∴B(8,0);
故答案为:(8,0);
(2)作AE⊥OB于E,DF⊥OB于F,
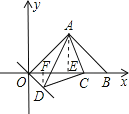
∵△ACD为等腰直角三角形,
∴AC=DC,∠ACD=90°
即∠ACF+∠DCF=90°,
∵∠FDC+∠DCF=90°,
∴∠ACF=∠FDC,
又∵∠DFC=∠AEC=90°,
∴△DFC≌△CEA,
∴EC=DF,FC=AE,
∵A(4,4),
∴AE=OE=4,
∴FC=OE,
即OF+EF=CE+EF,
∴OF=CE,
∴OF=DF,
∴∠DOF=45°
∵△AOB为等腰直角三角形,
∴∠AOB=45°,
∴∠AOD=∠AOB+∠DOF=90°;
(3)成立,理由如下:
在AM上截取AN=OF,连EN.

∵A(4,4),
∴AE=OE=4,
又∵∠EAN=∠EOF=90°,AN=OF,
∴△EAN≌△EOF(SAS)
∴∠OEF=∠AEN,EF=EN,
又∵△EGH为等腰直角三角形,
∴∠GEH=45°,
即∠OEF+∠OEM=45°,
∴∠AEN+∠OEM=45°
又∵∠AEO=90°,
∴∠NEM=45°=∠FEM,
又∵EM=EM,
∴△NEM≌△FEM(SAS),
∴MN=MF,
∴AM-MF=AM-MN=AN,
∴AM-MF=OF,
即![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习过程中遇到这样一个问题:如图1,在△ABC中,CA=CB,E是CD上一点,且ED=EB, ∠DEB=∠ACB,连接AD,探究∠ADC与∠DCB之间的数量关系.小明发现,∠ACD=∠CBE,CA=CB,因此可以通过作∠CAF=∠BCE交CD于点F构造全等,经过推理论证解决问题.
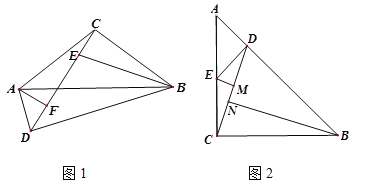
(1)按照小明思考问题的方法,解决问题;
(2)如图2,∠ACB=90,CA=CB,D是AB上一点,过点D作DE⊥AB交AC于点E,过点E作EM⊥CD于点M,BN⊥CD于点N,探究EM,BN,CD之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,顶点为(4,1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).
(1)求此抛物线的解析式;
(2)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积;
(3)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴
 与
与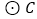 有怎样的位置关系,并给出证明.
有怎样的位置关系,并给出证明.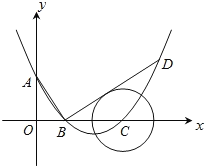
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )
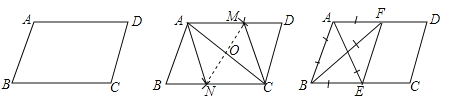
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是( ).
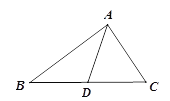
A. 2<AD<8B. 0<AD<8C. 1<AD<4D. 3<AD<5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片 ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、 AC于点E、G.连接GF.则下列结论错误的是( )
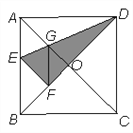
A. ∠AGD=112.5° B. 四边形AEFG是菱形 C. tan∠AED=2 D. BE=2OG
相关试题

