【题目】根据题意解答 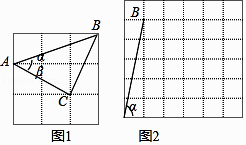
(1)如图1,如果ɑ,β都为锐角,且tanɑ= ![]() ,tanβ=
,tanβ= ![]() ,则ɑ+β=;
,则ɑ+β=;
(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ= ![]() 时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
参考答案:
【答案】
(1)45°
(2)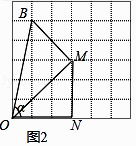 ;45
;45
【解析】解:(1)如图1中, 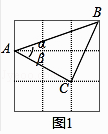
∵AC= ![]() ,BC=
,BC= ![]() ,AB=
,AB= ![]() ,
,
∴AC=BC,AC2+BC2=AB2 ,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∴α+β=45°.
所以答案是45°;
·(2)如图2中,
∵OB= ![]() ,MB=2
,MB=2 ![]() ,OM=3
,OM=3 ![]() ,
,
∴OB2=MB2+OM2 ,
∴∠BMO=90°,
∴tan∠MOB= ![]() ,
,
∴∠MOB=β,
∵∠OBN=α,
∴∠MON=α﹣β=45°.
所以答案是45.
【考点精析】根据题目的已知条件,利用解直角三角形的相关知识可以得到问题的答案,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
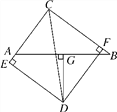
查看答案和解析>>【题目】如图,已知在△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,DG⊥AB,垂足分别是E,F,G.
(1)求证:AE=BF;
(2)求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
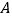 是反比例函数
是反比例函数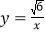 在第一象限图像上的一个动点,连接
在第一象限图像上的一个动点,连接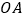 ,以
,以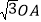 为长,
为长,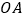 为宽作矩形
为宽作矩形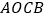 ,且点
,且点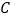 在第四象限,随着点
在第四象限,随着点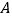 的运动,点
的运动,点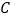 也随之运动,但点
也随之运动,但点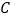 始终在反比例函数
始终在反比例函数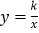 的图像上,则
的图像上,则 的值为( )
的值为( )
A.
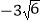 B.
B.  C.
C.  D.
D. 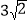
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
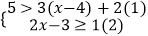 .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法. 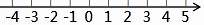
(1)解不等式(1),得;
(2)解不等式(2),得;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
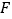 在平行四边形
在平行四边形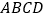 的边
的边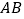 上,且
上,且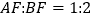 ,连接
,连接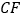 并延长,交
并延长,交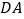 的延长线于点
的延长线于点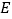 ,若
,若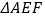 的面积为2,则平行四边形
的面积为2,则平行四边形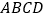 的面积为__________.
的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
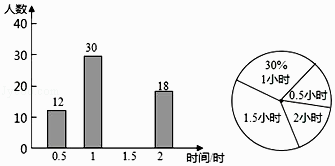
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 .
相关试题

