【题目】解不等式组: ![]() .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法. ![]()
(1)解不等式(1),得;
(2)解不等式(2),得;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为 .
参考答案:
【答案】
(1)x<5
(2)x≥2
(3)解:把不等式 (1)和 (2)的解集在数轴上表示为:
![]()
(4)2≤x<5
【解析】解:(1)去括号得,5>3x﹣12+2, 移项得,5+12﹣2>3x,
合并同类项得,15>3x,
把x的系数化为1得,x<5.
所以答案是:x<5;
·(2)移项得,2x≥1+3,
合并同类项得,2x≥4,
x的系数化为1得,x≥2.
所以答案是:x≥2;
·(4)由(3)得,原不等式的解集为:2≤x<5.
所以答案是:2≤x<5.
【考点精析】掌握不等式的解集在数轴上的表示和一元一次不等式组的解法是解答本题的根本,需要知道不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
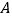 是反比例函数
是反比例函数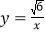 在第一象限图像上的一个动点,连接
在第一象限图像上的一个动点,连接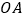 ,以
,以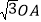 为长,
为长,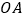 为宽作矩形
为宽作矩形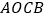 ,且点
,且点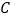 在第四象限,随着点
在第四象限,随着点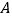 的运动,点
的运动,点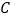 也随之运动,但点
也随之运动,但点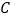 始终在反比例函数
始终在反比例函数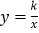 的图像上,则
的图像上,则 的值为( )
的值为( )
A.
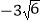 B.
B.  C.
C.  D.
D. 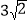
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
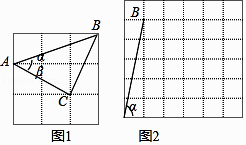
(1)如图1,如果ɑ,β都为锐角,且tanɑ= ,tanβ=
,tanβ=  ,则ɑ+β=;
,则ɑ+β=;
(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ= 时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
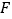 在平行四边形
在平行四边形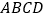 的边
的边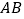 上,且
上,且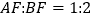 ,连接
,连接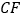 并延长,交
并延长,交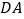 的延长线于点
的延长线于点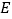 ,若
,若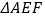 的面积为2,则平行四边形
的面积为2,则平行四边形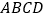 的面积为__________.
的面积为__________.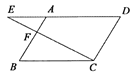
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
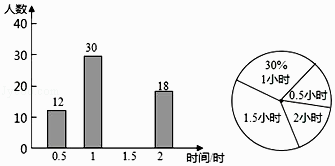
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.

(1)请你数一数,图中有 个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数= ,∠BOE的度数= ;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.
相关试题

