【题目】如图,△![]() 中,
中,![]() 、
、![]() 的角平分线
的角平分线![]() 、
、![]() 交于点
交于点![]() ,延长
,延长![]() 、
、![]() ,
,![]() ,
,![]() ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( )
①CP平分∠ACF; ②∠ABC+2∠APC=180°;
③∠ACB=2∠APB; ④若PM⊥BE,PN⊥BC,则AM+CN=AC;

A.1个B.2个C.3个D.4个
参考答案:
【答案】D
【解析】
①作PD⊥AC于D.由角平分线的性质得出PM=PN,PM=PD,得出PM=PN=PD,即可得出①正确;
②首先证出∠ABC+∠MPN=180°,证明Rt△PAM≌Rt△PAD(HL),得出∠APM=∠APD,同理:Rt△PCD≌Rt△PCN(HL),得出∠CPD=∠CPN,即可得出②正确;
③由角平分线和三角形的外角性质得出∠CAE=∠ABC+∠ACB,∠PAM=![]() ∠ABC+∠APB,得出∠ACB=2∠APB,③正确;
∠ABC+∠APB,得出∠ACB=2∠APB,③正确;
④由全等三角形的性质得出AD=AM,CD=CN,即可得出④正确;即可得出答案.
解:①作PD⊥AC于D.

∵PB平分∠ABC,PA平分∠EAC,PM⊥BE,PN⊥BF,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上,故①正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
在Rt△PAM和Rt△PAD中,
![]() ,
,
∴Rt△PAM≌Rt△PAD(HL),
∴∠APM=∠APD,
同理:Rt△PCD≌Rt△PCN(HL),
∴∠CPD=∠CPN,
∴∠MPN=2∠APC,
∴∠ABC+2∠APC=180°,②正确;
③∵PA平分∠CAE,BP平分∠ABC,
∴∠CAE=∠ABC+∠ACB,∠PAM=![]() ∠ABC+∠APB,
∠ABC+∠APB,
∴∠ACB=2∠APB,③正确;
④∵Rt△PAM≌Rt△PAD(HL),
∴AD=AM,
同理:Rt△PCD≌Rt△PCN(HL),
∴CD=CN,
∴AM+CN=AD+CD=AC,④正确;
故选:D.
-
科目: 来源: 题型:
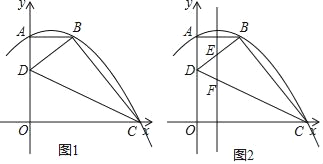
查看答案和解析>>【题目】已知,如图1,O是坐标原点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,AB⊥y轴于点A,AB=2,AO=4,OC=5,点D是线段AO上一动点,连接CD、BD.
(1)求出抛物线的解析式;
(2)如图2,抛物线的对称轴分别交BD、CD于点E、F,当△DEF为等腰三角形时,求出点D的坐标;
(3)当∠BDC的度数最大时,请直接写出OD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在AB上,点E在AC上,且∠AEB=∠ADC,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )

A.AD=AEB.∠B=∠CC.BE=CDD.AB=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
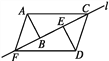
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】中雅培粹学校举办运动会,全校有3000名同学报名参加校运会,为了解各类运动赛事的分布情况,从中抽取了部分同学进行统计:A.田径类,B.球类,C.团体类,D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.

(1)这次统计共抽取了 位同学,扇形统计图中的
 ,
, 的度数是 ;
的度数是 ;(2)请将条形统计图补充完整;
(3)估计全校共多少学生参加了球类运动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
-
科目: 来源: 题型:
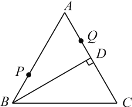
查看答案和解析>>【题目】如图,等边△
 中,
中, 于
于 ,
, ,点
,点 、
、 分别为
分别为 、
、 上的两个定点且
上的两个定点且 ,在
,在 上有一动点
上有一动点 使
使 最短,则
最短,则 的最小值为_____
的最小值为_____ .
.
相关试题

