【题目】如图,已知△ABC、△DEF都是正三角形,
(1)写出图中与∠AGF必定相等的角.
(2)对于(1)中的几个角,请你选择一个角证明与∠AGF相等(本小题将按照证明难度的大小分别给分,难度越大给分越多).
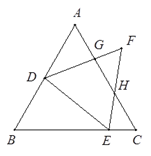
参考答案:
【答案】(1)∠DGH、∠ADE、∠BEH;(2)证明见试题解析.
【解析】试题分析:(1)易证∠AGF=∠F+∠FHG=60°+∠FHG,60°+∠FHG=∠C+∠EHC=∠BEH,得到∠AGF=∠BEH;由对顶角相等,得到∠DGH=∠AGF;在△ADG中,∠AGF=∠A+∠ADG=60°+∠ADG=∠EDG+∠ADG=∠ADE;
(2)由(1)的分析可得到证明过程.
试题解析:(1)∠DGH、∠ADE、∠BEH;
(2)证明∠AGF=∠DGH,∠AGF=∠ADE,∠AGF=∠BEH分别给1分,3分,5分.
①证明∠AGF=∠DGH,由对顶角相等,得到∠DGH=∠AGF;
②证明∠AGF=∠ADE,在△ADG中,∠AGF=∠A+∠ADG=60°+∠ADG=∠EDG+∠ADG=∠ADE,∴∠AGF=∠ADE;
③证明∠AGF=∠BEH,∵△ABC、△DEF均为正三角形,∴∠F=60°=∠C,∴∠AGF=∠F+∠GHF="∠C+" CHE=∠BEH.
-
科目: 来源: 题型:
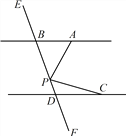
查看答案和解析>>【题目】如图,已知直线AB//CD,直线EF和直线AB,CD分别交于点B和点D,在直线 EF 上有一动点P.
(1).P点在线段BD上(点P 与点B,D不重合),请证明 :∠PAB+∠PCD=∠APC;
(2).若点P不在线段BD 上,请写出∠PAB, ∠PCD, ∠APC之间的数量关系,并画出相关图形,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
-
科目: 来源: 题型:
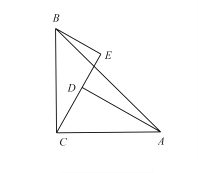
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE,垂足E,AD⊥CE, 垂足为 D,AD=2.5cm,BE=1.7cm,
(1).求证:△BCE≌△CAD
(2).求DE 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点位置如图所示.
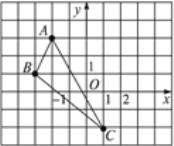
(1) 请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点);(3分)
(2) 直接写出△A′B′C′三点的坐标:A′_________,B′__________,C′_________.(3分)
(3)求A B′的长。(4分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】图形是由________,__________,____________构成的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是 ( )
A. 任意两个矩形形状相同 B. 任意两个菱形形状相同
C. 任意两个直角三角形相似 D. 任意两个正五边形形状相同
相关试题

