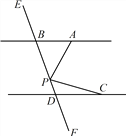
【题目】如图,已知直线AB//CD,直线EF和直线AB,CD分别交于点B和点D,在直线 EF 上有一动点P.
(1).P点在线段BD上(点P 与点B,D不重合),请证明 :∠PAB+∠PCD=∠APC;
(2).若点P不在线段BD 上,请写出∠PAB, ∠PCD, ∠APC之间的数量关系,并画出相关图形,说明理由.
参考答案:
【答案】(1)证明见解析;(2)当P点在射线BE上时,![]() ;当P点在射线DF 上时,
;当P点在射线DF 上时,![]() ,画图及证明见解析.
,画图及证明见解析.
【解析】试题分析:(1)过点P作PQ∥AB,根据平行公理求出PQ∥CD,再根据两直线平行,内错角相等可得∠APQ=∠PAB,∠CPQ=∠PCD,再根据∠APC=∠APQ+∠CPQ等量代换即可得证;(2)分点P在线段BD 的延长线上和点P在线段DB 的延长线上两种情况讨论∠PAB,∠PCD,∠APC之间的数量关系,过点P作PQ∥AB,然后根据类比(1)的方法探究证明即可.
试题解析:
(1) 过点P作PQ//AB .
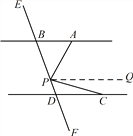
![]() ,
, ![]() .
.
![]() ,
,![]() ,
,
![]() .
.
(2) Ⅰ.如图,当P点在射线BE上时.
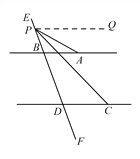
过点P作PQ//AB .
![]() ,
, ![]() .
.
![]() ,
,![]() ,
,
![]() .
.
Ⅱ.如图,当P点在射线DF 上时,
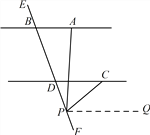
过点P作PQ//AB .
![]() ,
, ![]() .
.
![]()
![]() ,
, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-2)2000·22001的结果,正确的是( )
A. 2 B. -2 C. 24001 D. -24001
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚身高1.72m,他站立在阳光下的影子长为0.86m,紧接着他把手臂竖直举
起,影子长为1.15m,那么小刚举起的手臂超出头顶是_________m.
-
科目: 来源: 题型:
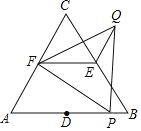
查看答案和解析>>【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
-
科目: 来源: 题型:
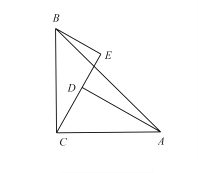
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE,垂足E,AD⊥CE, 垂足为 D,AD=2.5cm,BE=1.7cm,
(1).求证:△BCE≌△CAD
(2).求DE 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC、△DEF都是正三角形,
(1)写出图中与∠AGF必定相等的角.
(2)对于(1)中的几个角,请你选择一个角证明与∠AGF相等(本小题将按照证明难度的大小分别给分,难度越大给分越多).
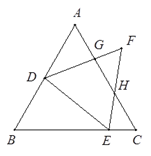
相关试题

