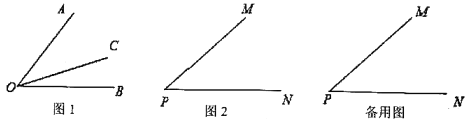
【题目】如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的三倍,则称射线OC是∠AOB的“奇分线”,如图2,∠MPN=42°:
(1)过点P作射线PQ,若射线PQ是∠MPN的“奇分线”,求∠MPQ;
(2)若射线PE绕点P从PN位置开始,以每秒8°的速度顺时针旋转,当∠EPN首次等于180°时停止旋转,设旋转的时间为![]() (秒).当
(秒).当![]() 为何值时,射线PN是∠EPM的“奇分线”?
为何值时,射线PN是∠EPM的“奇分线”?
参考答案:
【答案】(1)10.5°或14°或28°或31.5°;(2)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)分4种情况,根据奇分线定义即可求解;
(2)分4种情况,根据奇分线定义得到方程求解即可.
解:(1)如图1,∵∠MPN=42°,
∵当PQ是∠MPN的3等分线时,
∴∠MPQ=![]() ∠MPN=
∠MPN=![]() ×42°=14°
×42°=14°
或∠MPQ=![]() ∠MPN=
∠MPN=![]() ×42°=28°
×42°=28°
∵当PQ是∠MPN的4等分线时,
∴∠MPQ=![]() ∠MPN==
∠MPN==![]() ×42°=10.5°
×42°=10.5°
或∠MPQ=![]() ∠MPN=
∠MPN=![]() ×42°=31.5°;
×42°=31.5°;
∠MPQ=10.5°或14°或28°或31.5°;
(2)依题意有①当3×8t=42时,解得t=![]() ;
;
②当2×8t=42时,解得t=![]() ;
;
③当8t=2×42时,解得t=![]() .
.
④当8t=3×42时,解得:t=![]() ,
,
故当t为![]() 或
或![]() 或
或![]() 或
或![]() 时,射线PN是∠EPM的“奇分线”.
时,射线PN是∠EPM的“奇分线”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有__________.(选序号)
①若
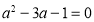 ,则
,则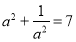 ;
;②若
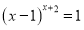 ,则满足条件
,则满足条件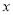 的值有3个;
的值有3个;③若
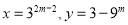 ,则用含
,则用含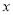 的代数式表示
的代数式表示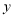 为
为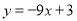 ;
;④若
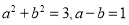 ,则
,则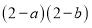 的值为
的值为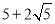 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是我校手工社团的一员,他在做折纸手工,如图所示在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点F是边CD上的任意一点,△AEF的周长最小时,则DF的长为( )
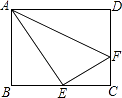
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
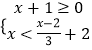 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.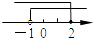
B.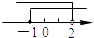
C.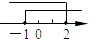
D.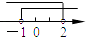
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )

A.
 B.
B. 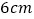 C.
C. 
 D.
D. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )
A.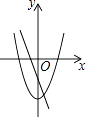
B.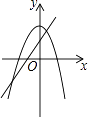
C.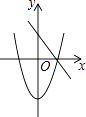
D.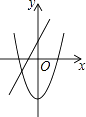
相关试题

