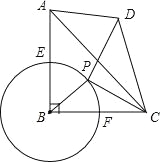
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B与AB、BC交于E、F,点P是弧EF上的一个动点,连接PC,线段PC绕P点逆时针旋转90°到PD,连接CD,AD.
(1)求证:△BPC∽△ADC;
(2)当四边形ABCD满足AD∥CB且是面积为12时,求⊙B的半径;
(3)若⊙B的半径的为2,当点P沿弧EF从点E运动至点PC与⊙B相切时,求点D的运动路径的长.
参考答案:
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)由等腰直角三角形的性质可知:BC:AC=PC:DC,∠PCD=∠ACB,从而可证明∠BCP=∠ACD,最后依据两边对应成比例且夹角相等的两三角形相似进行证明即可;
(2)如图1所示:先求得△ABC的面积,然后可得到△ADC的面积,依据三角形的面积公式可得到AD的长,然后依据相似三角形对应边长比例可求得PB的长;
(3)如图2所示:由相似三角形的性质可知:AD=2![]() ,于是可得到点D在以A为圆心,以2
,于是可得到点D在以A为圆心,以2![]() 为半径的圆上,然后根据点P在圆B的运动路线和确定点D经过的路径(弧)所对的圆心角,最后依据弧长公式求解即可.
为半径的圆上,然后根据点P在圆B的运动路线和确定点D经过的路径(弧)所对的圆心角,最后依据弧长公式求解即可.
试题解析:(1)∵∠ABC=90°,AB=BC,
∴∠ACB=45°,BC:AC=1:![]() .
.
∵PD=PC,∠DPC=90°,
∴∠PCD=45°,PC:DC=1:![]() .
.
∴BC:AC=PC:DC,∠PCD=∠ACB.
∴∠PCD﹣∠PCA=∠ACB﹣∠PCA,即∠BCP=∠ACD.
∴△BPC∽△ADC.
(2)如图1所示:

∵AB=BC=4,∠ABC=90°,
∴S△ABC=![]() ABBC=
ABBC=![]() ×4×4=8,
×4×4=8,
∵四边形ABCD的面积为12,
∴S△ADC=4.
∵AD∥BC,
∴S△ADC=![]() ADAB=4,即
ADAB=4,即![]() ×4×AD=4.
×4×AD=4.
∴AD=2.
∵△BPC∽△ADC,
∴![]() ,
,
即![]() .
.
解得BP=![]() .
.
∴⊙B的半径为![]() .
.
(3)如图2所示:

∵BP=2,由(2)可知AD:BP=![]() :1,
:1,
∴AD=2![]() .
.
∴D在以A为圆心,以2![]() 为半径的圆上.
为半径的圆上.
∵△BPC∽△ADC,
∴∠PBC=∠DAC.
∵当点P与点E重合时,∠PBC=90°.
∴∠DAC=90°.
当点P′C与圆B相切时,∠BP′C=90°,BP′=2,BC=4,
∴∠P′BC=60°.
span>∴∠D′AC=60°.
∴∠D′AD=90°﹣60°=30°.
∴点D运动的路线长=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )

A.110°
B.100°
C.90°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律.则第(6)个图形中面积为1的正方形的个数为( )
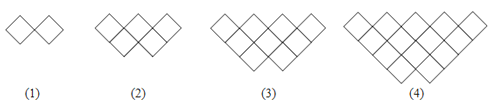
A.20
B.27
C.35
D.40 -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2+2x﹣1向上平移4个单位后,所得新抛物线的顶点坐标是 .
-
科目: 来源: 题型:
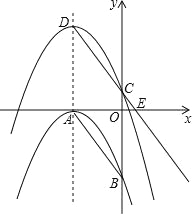
查看答案和解析>>【题目】如图,抛物线C1:y=﹣
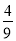 (x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,(1)求A,B点的坐标;
(2)当CE:CD=1:2时,求此时抛物线C2的顶点坐标;
(3)若四边形ABCD是菱形.
①此时抛物线C2的解析式;
②点F在抛物线C2的对称轴上,且点F在第三象限,点M在抛物线C2上,点P是坐标平面内一点,是否存在以A,F,P,M为顶点的四边形与菱形ABCD相似,并且这个菱形以A为顶点的角是钝角,若存在求出点F的坐标,若不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个数:1、-2、0、-3,其中最小的一个是( )
A. 1 B. -2 C. 0 D. -3
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣1)2015﹣2﹣2+30
(2)x(x﹣y)﹣(x+2y)(2x﹣y)
相关试题

