搜索
【题目】如图，点
在等边
的边
上，
，射线
于点
，点
是射线
上一动点，点
是线段
上一动点，当
的值最小时，
，则
为( )
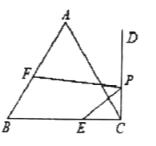
A. 14B. 13C. 12D. 10
参考答案：
【答案】D
【解析】
根据等边三角形的性质得到AC=BC，∠B=60°，作点E关于直线CD的对称点G，过G作GF⊥AB于F，交CD于P，则此时，EP+PF的值最小，根据直角三角形的性质得到BG=2BF=14，求得EG=8，于是得到结论．
解：∵△ABC是等边三角形，
∴AC=BC，∠B=60°，
作点E关于直线CD的对称点G，过G作GF⊥AB于F，交CD于P，
则此时，EP+PF的值最小，
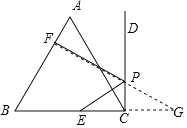
∵∠B=60°，∠BFG=90°，
∴∠G=30°，
∵BF=7，
∴BG=2BF=14，
∴EG=8，
∵CE=CG=4，
∴AC=BC=10，
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某小区积极创建环保示范社区，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，已知温馨提示牌的单价为每个30元，垃圾箱的单价为每个90元，共需购买温馨提示牌和垃圾箱共100个.
（1）若规定温馨提示牌和垃圾箱的个数之比为1:4，求所需的购买费用；
（2）若该小区至多安放48个温馨提示牌，且费用不超过6300元，请列举所有购买方案，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】现在全省各大景区都在流行“真人CS“娱乐项目，其中有一个“快速抢点”游戏，游戏规则：如图，用绳子围成的一个边长为10m的正方形ABCD场地中，游戏者从AB边上的点E处出发，分别先后赶往边BC、CD、DA上插小旗子，最后回到点
已知
，则游戏者所跑的最少路程是多少______
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
（1）出发2秒后，求PQ的长.
（2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？
（3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出下列四个命题：
①设有一批产品，其次品率为0.05，则从中任取200件，必有10件是次品；
②做100次抛硬币的试验，结果51次出现正面朝上，因此，出现正面朝上的概率是
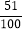；③随机事件发生的频率就是这个随机事件发生的概率；
④抛掷骰子100次，得点数是1的结果18次，则出现1点的频率是
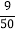.其中正确命题有________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．
我们有多少种剪法，图1是其中的一种方法：
定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
（1）请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
（2）△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并求出x所有可能的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠A=
,∠B=
，CD是AB边上的高；CE是∠ACB的平分线，DF⊥CE于F，求∠BCE和∠CDF的度数.
相关试题
