【题目】(12分)(1)如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标_____(用含a的代数式表示);
(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.
(3)如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.

参考答案:
【答案】(1)N(2+a,a);(2)见解析;(3)见解析.
【解析】 (1)如图1中,作NE⊥OB于E,只要证明△DMO≌△MNE,即可解决问题.
(2)如图2中,在OD上取OH=OM,连接HM,只要证明△DHM≌△MBN即可.
(3)结论:MN平分∠FMB成立.如图3中,在BO延长线上取OA=CF,过M作MP⊥DN于P,因为∠NMB+∠CDF=45°,所以只要证明∠FMN+∠CDF=45°即可解决问题.
解:(1)解:如图1中,作NE⊥OB于E,

∵∠DMN=90°,
∴∠DMO+∠NME=90°,∠NME+∠MNE=90°,
∴∠DMO=∠MNE,
在△DMO和△MNE中,
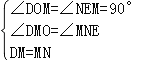 ,
,
∴△DMO≌△MNE,
∴ME=DO=2,NE=OM=a,
∴OE=OM+ME=2+a,
∴点N坐标(2+a,a),
故答案为N(2+a,a).
(2)证明:如图2中,在OD上取OH=OM,连接HM,
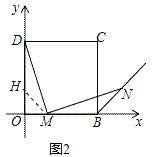
∵OD=OB,OH=OM,
∴HD=MB,∠OHM=∠OMH,
∴∠DHM=180°﹣45°=135°,
∵NB平分∠CBE,
∴∠NBE=45°,
∴∠NBM=180°﹣45°=135°,
∴∠DHM=∠NBM,
∵∠DMN=90°,
∴∠DMO+∠NMB=90°,
∵∠HDM+∠DMO=90°,
∴∠HDM=∠NMB,
在△DHM和△MBN中,
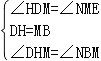 ,
,
∴△DHM≌△MBN(ASA),
∴DM=MN.
(3)结论:MN平分∠FMB成立.
证明:如图3中,在BO延长线上取OA=CF,
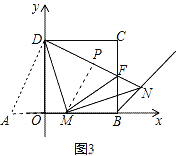
在△AOD和△FCD中,
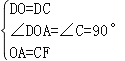 ,
,
∴△DOA≌△DCF,
∴AD=DF,∠ADO=∠CDF,
∵∠MDN=45°,
∴∠CDF+∠ODM=45°,
∴∠ADO+∠ODM=45°,
∴∠ADM=∠FDM,
在△DMA和△DMF中,
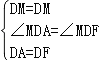 ,
,
∴△DMA≌△DMF,
∴∠DFM=∠DAM=∠DFC,
过M作MP⊥DN于P,则∠FMP=∠CDF,
由(2)可知∠NMF+∠FMP=∠PMN=45°,
∴∠NMB=∠MDH,∠MDO+∠CDF=45°,
∴∠NMB=∠NMF,即MN平分∠FMB.
“点睛”本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质,解题的关键是学会添加辅助线,构造全等三角形,记住一些基本图形,可以使得我们在观察新问题的时候很迅速地联想,属于中考压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小雨写了几个多项式,其中是五次三项式的是( )
A. y5-1 B. 5x2y2-x+y C. 3a2b2c-ab+1 D. 3a5b-b+c
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a-b=3,c+d=2,则(b+c)-(a-d)的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将四张分别写有数字1,2,3,4的红色卡片放在一个不透明的盒中,三张分别写有数字1,2,3的蓝色卡片放在另一个不透明的盒中,卡片除颜色和数字外完全相同.现从两个盒内各任意抽取一张卡片,以红色卡片上的数字作为十位数字,蓝色卡片上的数字作为个位数字组成一个两位数.
(1)求组成的两位数是偶数的概率;
(2)求组成的两位数大于22的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体中,正视图、左视图、俯视图完全相同的是
A. 圆柱 B. 圆锥
C. 棱锥 D. 球
-
科目: 来源: 题型:
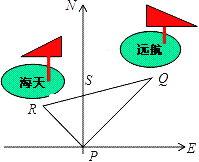
查看答案和解析>>【题目】(9分)如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile
(1)求PQ,PR的长度;
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. 3a+2b=5ab B. 2a3+3a2=5a5
C. 3a2b-3ba2=0 D. 5a2-4a2=1
相关试题

