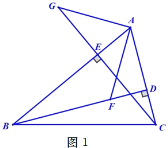
【题目】如图,在△ABC中,BD,CE分别是AC,AB边上的高,在BD上截取BF=AC,延长CE至点G使CG=AB,连接AF,AG.
(1)如图1,求证:AG=AF;
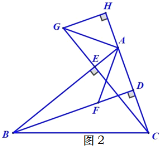
(2)如图2,若BD恰好平分∠ABC,过点G作GH⊥AC交CA的延长线于点H,请直接写出图中所有的全等三角形并用全等符号连接.
参考答案:
【答案】(1)证明见解析;(2)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据![]() 、
、![]() 分别是
分别是![]() 、
、![]() 两条边上的高,BF=AC,CG=AB,利用SAS可证
两条边上的高,BF=AC,CG=AB,利用SAS可证![]() ,则可证
,则可证![]() ;
;
(2)利用等腰三角形的对称性,可得![]() ;根据
;根据![]() 易证
易证![]() ,则可得
,则可得![]() ,即有
,即有![]() ,利用AAS可证
,利用AAS可证![]() .
.
(1)证明:∵![]() 、
、![]() 分别是
分别是![]() 、
、![]() 两条边上的高,
两条边上的高,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,
 ,
,
![]() ,
,
∴![]() ;
;
(2)∵BD平分∠ABC,BD是AC边上的高,
则BD为△ABC中三线合一的线,即△ABC为等腰三角形,BD为△ABC的对称轴,
根据对称性,有![]()
![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∴![]()
在![]() 与
与![]() 中,
中,
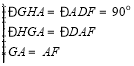 ,
,
![]() ,
,
综上所述,全等三角形有![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。



-
科目: 来源: 题型:
查看答案和解析>>【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(cos230°+sin230°)×tan60°
(2)解方程:x2﹣2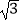 x﹣1=0.
x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】“双11”期间,某个体户在淘宝网上购买某品牌A、B两款羽绒服来销售,若购买3件A,4件B需支付2400元,若购买2件A,2件B,则需支付1400元.
(1)求A、B两款羽绒服在网上的售价分别是多少元?
(2)若个体户从淘宝网上购买A、B两款羽绒服各10件,均按每件600元进行零售,销售一段时间后,把剩下的羽绒服全部6折销售完,若总获利不低于3800元,求个体户让利销售的羽绒服最多是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在第一象限,点B(a,0),点C(0,b)分别在x轴,y轴上,其中a,b是二元一次方程
 的解,且a为不等式
的解,且a为不等式 的最大整数解.
的最大整数解.(1)证明:OB=OC;
(2)如图1,连接AB,过点A作AD⊥AB交y轴于点D,在射线AD上截取AE=AB,连接CE,取CE的中点F,连接AF并延长至点G,使FG=AF,连接CG,OA.当点A在第一象限内运动(AD不经过点C)时,证明:∠OAF的大小不变;

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中,共有“一白三黑”四个围棋子,其除颜色外无其他区别.
(1)随机地从盒子中取出1子,则提出的是白子的概率是多少?
(2)随机地从盒子中取出1子,不放回再取出第二子,请用画树状或列表的方式表示出所有可能的结果,并求出恰好取出“一黑一白”的概率是多少?
相关试题

