【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;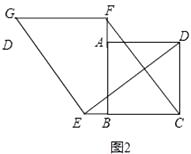
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.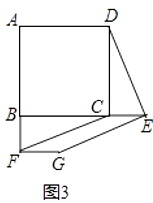
参考答案:
【答案】
(1)解:结论:FG=CE,FG∥CE.
理由:如图1中,设DE与CF交于点M.
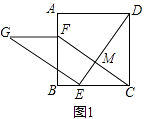
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
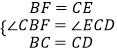 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
(2)解:结论仍然成立.
理由:如图2中,设DE与CF交于点M.
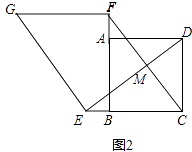
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
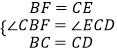 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
(3)解:结论仍然成立.
理由:如图3中,设DE与FC的延长线交于点M.
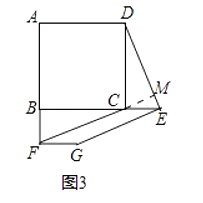
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
∴∠CBF=∠DCE=90°
在△CBF和△DCE中,
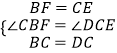 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
【解析】(1)结论:FG=CE,FG∥CE.如图1中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(2)结论仍然成立.如图2中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(3)结论仍然成立.如图3中,设DE与FC的延长线交于点M,证明方法类似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:
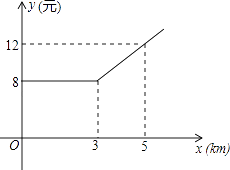
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2x3=x6
B.5x﹣2x=3x
C.(x2)3=x5
D.(﹣2x)2=﹣4x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(-x3)4+(-2x6)2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=3是方程ax﹣2=-a+6的解,则a=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2﹣1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用乘法公式计算:
(1)1972 (2)20092-2008×2010
相关试题

