【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
参考答案:
【答案】
(1)证明:如图,∵AD⊥CE,∠ACB=90°,
∴∠ADC=∠ACB=90°,
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中,
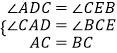 ,
,
∴△ADC≌△CEB(AAS)
(2)由(1)知,△ADC≌△CEB,则AD=CE=5cm,CD=BE.
如图,∵CD=CE﹣DE,
∴BE=AD﹣DE=5﹣3=2(cm),即BE的长度是2cm
【解析】(1)根据全等三角形的判定定理AAS推知:△ADC≌△CEB;(2)利用(1)中的全等三角形的对应边相等得到:AD=CE=5cm,CD=BE.则根据图中相关线段的和差关系得到BE=AD﹣DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件商品的原价是100元,经过两次提价后的价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
A.100(1+x)=121
B.100(1﹣x)=121
C.100(1+x)2=121
D.100(1﹣x)2=121 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足表格:
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则该函数图象的顶点坐标为( )
A.(﹣4,﹣6)
B.(﹣2,﹣2)
C.(﹣1,﹣3)
D.(0,﹣6) -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=3x2+1向左平移1个单位,再向下平移3个单位,则所得抛物线为( )
A. y=3(x+1)2+2B. y=3(x+1)2﹣2
C.y=3(x﹣3)2+1D.y=3(x﹣3)2﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
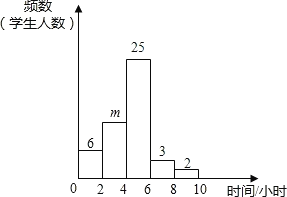
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生(其中6~8小时的3人分别用
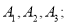 8~10分别用
8~10分别用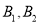 表示)中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.
表示)中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AC=BD时,它是矩形B.当AC⊥BD时,它是菱形
C.当∠A=60°时,它是菱形D.当AB=BC,AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】东营市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收1.5元(不足1千米按1千米计).某人从甲地到乙地经过的路程是x千米,出租车费为15.5元,那么x的最大值是( )
A. 11 B. 8 C. 7 D. 5
相关试题

