【题目】如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是 . 
参考答案:
【答案】10cm,2 ![]() cm,4
cm,4 ![]() cm
cm
【解析】解:如图: 
过点A作AD⊥BC于点D,
∵△ABC边AB=AC=10cm,BC=12cm,
∴BD=DC=6cm,
∴AD=8cm,
如图①所示:
可得四边形ACBD是矩形,则其对角线长为:10cm,
如图②所示:AD=8cm,
连接BC,过点C作CE⊥BD于点E,
则EC=8cm,BE=2BD=12cm,
则BC=4 ![]() cm,
cm,
如图③所示:BD=6cm,
由题意可得:AE=6cm,EC=2BE=16cm,
故AC= ![]() =2
=2 ![]() cm,
cm,
所以答案是:10cm,2 ![]() cm,4
cm,4 ![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( )
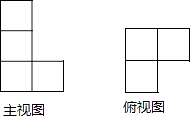
A.10
B.11
C.12
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的侧面积是底面积的3倍,则这个圆锥侧面展开图的圆心角度数为( )
A.120°
B.180°
C.240°
D.300° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(﹣
 ,y1),(﹣
,y1),(﹣  ,y2),(﹣
,y2),(﹣  ,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( )
,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( ) 
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=
 ,反比例函数y=
,反比例函数y=  的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3 , 以OA3为直角边作第三个等腰直角三角形OA3A4 , …,依此规律,得到等腰直角三角形OA2017A2018 , 则点A2017的坐标为 .

相关试题

