【题目】阅读理解:
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是![]() ,
,![]() .
.
![]() 对于坐标平面内的一点P,给出如下定义:如果
对于坐标平面内的一点P,给出如下定义:如果![]() ,则称点P为线段AB的“等角点”
,则称点P为线段AB的“等角点”![]() 显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
![]() 设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和
设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和![]() 的半径;
的半径;
![]() 轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
![]() 当点P在y轴正半轴上运动时,
当点P在y轴正半轴上运动时,![]() 是否有最大值?如果有,说明此时
是否有最大值?如果有,说明此时![]() 最大的理由,并求出点P的坐标;如果没有请说明理由.
最大的理由,并求出点P的坐标;如果没有请说明理由.
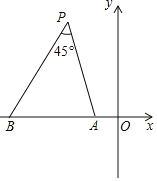
参考答案:
【答案】(1)①![]() 或
或![]() ,半径为
,半径为![]() ,②
,②![]() ,
,![]() .(2)
.(2)![]()
【解析】分析:
(1)①如下图1,连接BC、AC,则由“圆周角定理”可知∠ACB=2∠APB=90°,过点C作CH⊥AB于点H,则由已知条件根据“垂径定理”可得AH=BH=CH=3,从而可得OH=OA+AH=4,由此即可得到点C的坐标为(-4,3)或(-4,-3);此时在Rt△ACH中由勾股定理可求得![]() 的半径为
的半径为![]() ;②如下图2,当点C的坐标为(-4,3)时,过点C作CD⊥y轴于点D,则由CD=4<
;②如下图2,当点C的坐标为(-4,3)时,过点C作CD⊥y轴于点D,则由CD=4<![]() 可知,此时
可知,此时![]() C和y轴有交点,设交点为P1和P2,连接CP1和CP2,利用勾股定理求得DP1和DP2的长度即可求得P1和P2的坐标了;
C和y轴有交点,设交点为P1和P2,连接CP1和CP2,利用勾股定理求得DP1和DP2的长度即可求得P1和P2的坐标了;
(2)如下图3,当过A,B的圆与y轴相切于点P时,∠![]() 最大,设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点
最大,设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点![]() 不与点P重合
不与点P重合![]() ,连接MA,MB,PA,PB,设MB交
,连接MA,MB,PA,PB,设MB交![]() E于点N,连接NA,则由“圆周角定理”和“三角形外角的性质”易得∠APB=∠ANB>∠AMB,从而说明此时∠APB最大;再过点E作EF⊥x轴于点F,连接EA、EP,易证四边形OPEF是矩形,由此可得PE=OF=4,再Rt△AEF中,由勾股定理可得EF=
E于点N,连接NA,则由“圆周角定理”和“三角形外角的性质”易得∠APB=∠ANB>∠AMB,从而说明此时∠APB最大;再过点E作EF⊥x轴于点F,连接EA、EP,易证四边形OPEF是矩形,由此可得PE=OF=4,再Rt△AEF中,由勾股定理可得EF=![]() ,从而可得OP=
,从而可得OP=![]() ,由此即可得到此时点P的坐标为
,由此即可得到此时点P的坐标为![]() .
.
详解:
(1)①如图1,
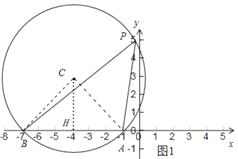
在x轴的上方,作以AB为斜边的直角三角形ACB,易知点A,B,P在![]() 上,连接
上,连接![]() 轴于点H,
轴于点H,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由垂径定理可得,![]() ,
,
∴![]() ,
,![]() ,
,
所以![]() ,半径为
,半径为![]() ,
,
由对称性可知,点![]() 也满足条件.
也满足条件.
②![]() 轴的正半轴上存在线段AB的“等角点”.
轴的正半轴上存在线段AB的“等角点”.
如图2所示,

当圆心为![]() 时,过点C作
时,过点C作![]() 轴于点D,则
轴于点D,则![]() ,
,![]() ,
,
∵![]() 的半径为
的半径为![]() ,
,
∴![]() 与y轴相交,
与y轴相交,
设交点为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,CA,则
,CA,则![]() ,
,
∵![]() 轴,
轴,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
![]() 当过A,B的圆与y轴相切于点P时,
当过A,B的圆与y轴相切于点P时,![]() 最大.
最大.
理由如下:如果点P在y轴的正半轴上,如图3,
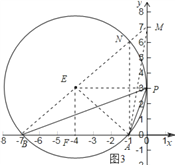
设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点![]() 不与点P重合
不与点P重合![]() ,
,
连接MA,MB,PA,PB,设MB交![]() 于点N,连接NA,
于点N,连接NA,
∵点P、点N在![]() 上,
上,
∴![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,即
,即![]() ,
,
此时,过点E作![]() 轴于点F,连接EA,EP,则
轴于点F,连接EA,EP,则![]() ,
,![]() ,
,
∵![]() 与y轴相切于点P,则
与y轴相切于点P,则![]() 轴,
轴,
∴四边形OPEF是矩形,![]() ,
,![]() ,
,
∴![]() 的半径为4,即
的半径为4,即![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
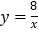 与一次函数
与一次函数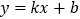 的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是
的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是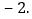 求:
求: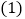 一次函数的解析式;
一次函数的解析式;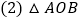 的面积;
的面积; 直接写出使反比例函数的值大于一次函数的值的x的取值范围.
直接写出使反比例函数的值大于一次函数的值的x的取值范围.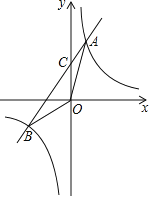
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过三边都不相等的三角形的一个顶点的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线
(2)在△ABC中,∠A=52°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=3,BC=2,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
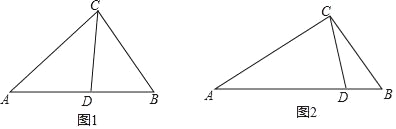
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为
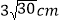 ,则这块圆形纸片的直径为( )
,则这块圆形纸片的直径为( )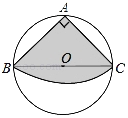
A. 12cm B. 20cm C. 24cm D. 28cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
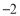 ,4,
,4,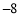 ,16,
,16, …,①
…,①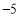 ,1,
,1,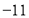 ,13,
,13,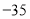 …,②
…,②4,
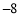 ,16,
,16, ,64,…,③
,64,…,③(1)第①行第7个数_________________;
(2)第②、③行数与第①行数分别有什么关系?
(3)取每行数的第8个数,计算这三个数的和.
相关试题

