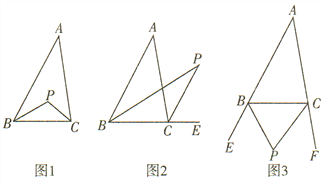
【题目】在△ABC中,∠A=40°.
(1)如图1,若两内角∠ABC,∠ACB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(2)如图2,若内角∠ABC,外角∠ACE的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(3)如图3,若两外角∠EBC,∠FCB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 .
(选择其中一种数量关系加以证明)
参考答案:
【答案】(1)∠P=90°+![]() ∠A;(2)∠P=
∠A;(2)∠P=![]() ∠A;(3)70°;∠P=90°-∠A.
∠A;(3)70°;∠P=90°-∠A.
【解析】试题分析:(1)根据三角形内角和定理求出∠B和∠C,再根据角平分线的性质和三角形内角和是180°求出∠P=180°-![]() (∠B+∠C);
(∠B+∠C);
(2)根据三角形的一个外角等于和它不相邻的两个内角的和以及叫平分线的性质可求出∠P,可得∠A与∠P之间的数量关系;
(3)根据三角形的一个外角等于和它不相邻的两个内角的和求得:∠EBC+∠BCF=∠A+∠ACB+∠ABC+∠A=180°+∠A,在△BCP中根据角平分线的定义以及三角形内角和定理即可求解.
试题解析:(1)∠ABC+∠C=180°∠A=180°40°=140°
∴![]() (∠ABC+∠C)=
(∠ABC+∠C)=![]() ×140°=70°,
×140°=70°,
∴∠P=180°![]() (∠ABC+∠C)=110°.
(∠ABC+∠C)=110°.
∠A与∠P之间的数量关系是∠P=90°+![]() ∠A;
∠A;
(2)∵![]() ∠ACE=
∠ACE=![]() ∠ABC+∠P,
∠ABC+∠P,
∴![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() ∠ABC+∠P,
∠ABC+∠P,
∴![]() (40°+∠ABC)=
(40°+∠ABC)=![]() ∠ABC+∠P,
∠ABC+∠P,
∴∠P=20°.
∠A与∠P之间的数量关系是∠P=![]() ∠A;
∠A;
(3)∵∠EBC=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴∠EBC+∠BCF=∠A+∠ACB+∠ABC+∠A=180°+∠A,
∴∠PBC+∠PCB=90°+![]() ∠A.
∠A.
又∵∠PBC+∠PCB+∠P=180°,
∴90°+![]() ∠A+∠P=180°,即∠P=90°
∠A+∠P=180°,即∠P=90°![]() ∠A,
∠A,
当∠A=40°时,∠P=70°.
-
科目: 来源: 题型:
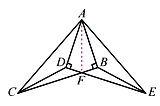
查看答案和解析>>【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3y2﹣12=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-3x2y2)2(2xy)3÷(xy)2=____________.
-
科目: 来源: 题型:
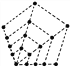
查看答案和解析>>【题目】观察下面的点阵图形和与之相对应的等式,探究其中的规律:
(1)请你在④和⑤后面的横线上分别写出相对应的等式.
①·4×0+1=4×1-3;
②
 4×1+1=4×2-3;
4×1+1=4×2-3;③
 4×2+1=4×3-3;
4×2+1=4×3-3;④
 ______________;
______________;⑤
 ______________;
______________;(2)通过猜想,写出与第
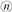 个图形相对应的等式.
个图形相对应的等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需________根火柴( )

A. 156 B. 157 C. 158 D. 159
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式a﹣3b=﹣5,则代数式6﹣a+3b的值是( )
A. 0 B. 6 C. 8 D. 11
相关试题

