【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.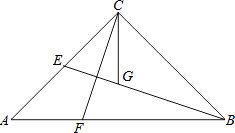
(1)求证:CF=BG;
(2)延长CG交AB于点H,判断点G是否在线段AB的垂直平分线上?并说明理由.
(3)过点A作AD⊥AB交BE的延长线于点D,请证明:CF=2DE.
参考答案:
【答案】
(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∵CG平分∠ACB,
∴∠BCG=45°=∠A,
∴∠BCG=∠CAB=45°,
在△ACF和△BCG中,  ,
,
∴△ACF≌△BCG(ASA),
∴AF=CG,CF=BG
(2)解:点G在线段AB的垂直平分线上,如图1所示:理由如下:

∵AC=BC,CG平分∠ACB,
∴CH⊥AB,H为AB中点,
∴点G在线段AB的垂直平分线上
(3)证明:连接AG.如图2所示:

由(2)可知,AG=BG,∠GAB=∠GBA,
∵AD⊥AB,
∴∠GAB+∠GAD=∠GBA+∠D=90°,
∴∠GAD=∠D,
∴GA=GD=GB=CF.
∵AD⊥AB,CH⊥AB
∴CH∥AD,
∴∠D=∠EGC,
∵E为AC中点,
∴AE=EC,
在△AED和△CEG中,  ,
,
∴△AED≌△CEG(SAS),
∴DE=EG,
∴DG=2DE,
∴CF=2DE
【解析】 (1)根据等腰直角三角形的性质及角平分线的定义得出∠BCG=∠CAB=45°,然后由ASA判断出△ACF≌△BCG,然后根据全等三角形的性质得出结论;
(2)根据等腰三角形的三线合一得出CH⊥AB,H为AB中点,故点G在线段AB的垂直平分线上;
(3)连接AG,由垂直的定义得出∠GAD=∠D, 根据等边对等角得出GA=GD=GB=CF,由平行线的判定得出CH∥AD,故∠D=∠EGC,然后由SAS得出△AED≌△CEG,根据全等三角形的性质得出结论。
【考点精析】根据题目的已知条件,利用平行线的判定与性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
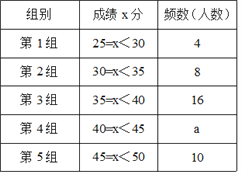
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
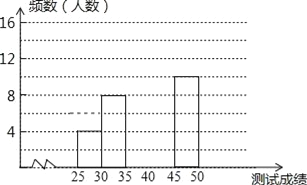
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九(三)班的演唱打分情况为:89,92,92,95,95,96,97,从中去掉一个最高分和一个最低分,余下的分数的平均数是最后得分,则该班的得分为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=﹣
 x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.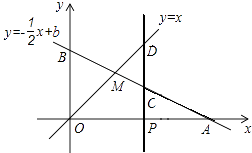
(1)求点A的坐标;
(2)在x轴上有一点动点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ x+b和y=x的图象于点C、D,且OB=2CD,求a的值.
x+b和y=x的图象于点C、D,且OB=2CD,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2014年,我国国内生产总值约为636000亿元,用科学记数法表示2014年国内生产总值约为亿元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两条边的长分别为3和1,则该等腰三角形的周长为( )
A. 5B. 7C. 5或7D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x2y﹣xy)﹣3(x2y﹣2xy)+4x2y,其中x=﹣1,y=2.
相关试题

