【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=![]() .
.
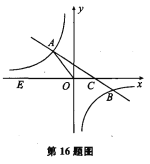
【1】求该反比例函数和一次函数的解析式
【2】求△AOC的面积
参考答案:
【答案】
【1】y=-![]() x+2;
x+2;
【2】6
【解析】:(1)过点A作AD⊥x轴于D点,如图,
∵sin∠AOE=![]() ,OA=5,
,OA=5,
∴sin∠AOE=![]() =
=![]() ,
,
∴AD=4,
∴DO=![]() =3,
=3,
而点A在第二象限,
∴点A的坐标为(-3,4),
将A(-3,4)代入y=![]() ,得m=-12,
,得m=-12,
∴反比例函数的解析式为y=-![]() ;
;
将B(6,n)代入y=-![]() ,得n=-2;
,得n=-2;
将A(-3,4)和B(6,-2)分别代入y=kx+b(k≠0),得
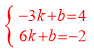 ,
,
解得,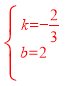
∴所求的一次函数的解析式为y=-![]() x+2;
x+2;
(2)在y=-![]() x+2中,令y=0,
x+2中,令y=0,
即-![]() x+2=0,
x+2=0,
解得x=3,
∴C点坐标为(3,0),即OC=3,
∴S△AOC=![]() ADOC=
ADOC=![]() 43=6.
43=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打笫一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点.已知∠AEG=∠AGE,∠DCG=∠DGC.

(1) 求证:AB∥CD
(2) 若∠AGE+∠AHF=180°,且∠BFC-30°=2∠C,求∠B的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一个正方体的表面展开图,请回答下列问题:

(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+
 a2b+3,B=﹣
a2b+3,B=﹣ a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣ (a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
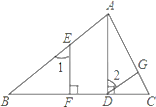
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
相关试题

