【题目】某网店销售一种成本价为每件60元的商品,规定销售期间销售单价不低于成本价,且每件获利不得高于成本价的45%.经测算,每天的销售量y(件)与销售单价x(元)的关系符合一次函数y=﹣x+120,设该网店每天销售该商品所获利润为W(元).
(1)试写出利润W与销售单价x之间的函数关系式;
(2)销售单价定为多少元时,该网店每天销售该商品可获得最大利润,最大利润是多少元?
(3)若该网店每天销售该商品所获利润不低于500元,请直接写出销售单价x的范围.
参考答案:
【答案】(1)W=-x2+180x-7200(60≤x≤87);(2) 销售单价定为87元时,商场可获得最大利润,最大利润是891元;(3) 销售单价的范围为70(元)≤x≤87(元)时,该商场获得利润不低于500元.
【解析】试题分析:(1)先根据题意求出x的范围,再根据公式每天销售该商品所获利润=每天的销量×每件商品的利润写出利润W与销售单价x之间的函数关系式;(2)由于W是关于x的二次函数,将函数写成顶点式,在x的范围内根据函数的增减性求出最大值即可;(3)令W=500,解出x,再根据函数的增减性判断出x的范围.
试题解析:
(1)∵成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,即不高于60(1+45%)=87,
∴60≤x≤87;
W=(x-60)y=(x-60)(-x+120)
=-x2+180x-7200(60≤x≤87);
(2)W=-![]() +900,
+900,
∵a=-1<0,
∴当x<90时,W随x的增大而增大,
∴x=87时,W有最大值,其最大值=891,
即销售单价定为87元时,商场可获得最大利润,最大利润是891元;
(3)令W=500,则-![]() +900=500,解得x1=70,x2=110,
+900=500,解得x1=70,x2=110,
∵当x<90时,W随x的增大而增大,
∴当销售单价的范围为70(元)≤x≤87(元)时,该商场获得利润不低于500元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《教育导报》记者就四川省农村中小学教师阅读状况进行了一次问卷调查,并根据调查结果绘制了教师每年阅读书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本).其中A:1x3; B:4x6; C:7x9;D:x10.请你根据两幅图提供的信息解答下列问题:
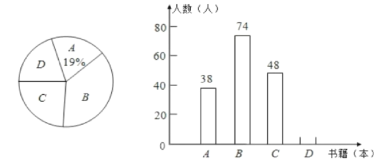
(1)本次共调查了多少名教师?
(2)补全条形统计图;
(3)计算扇形统计图中扇形D的圆心角的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
-
科目: 来源: 题型:
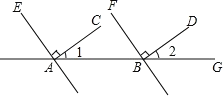
查看答案和解析>>【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌店购进A种衬30件和B种衬衫40件共用了9600元,购进A种衬衫40件和B种衬衫20件共用了7800元.
(1)A、B两种衬衫的单价分别是多少元?
(2)已知该品牌店购进B种衬衫的件数比A种衬衫的件数的2倍少2件,如果购进A、B两种衬衫的总件数不少于97件,且该品牌购进A、B两种衬衫的总费用不超过13980元,那么该品牌店有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图像与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
的图像与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).(1)求二次函数的表达式;
(2)设上述抛物线的对称轴l与x轴交于点D,过点C作CE⊥l于E,P为线段DE上一点,Q(m,0)为x轴负半轴上一点,以P、Q、D为顶点的三角形与△CPE相似;
①当满足条件的
 点有且只有三个时,求
点有且只有三个时,求 的取值范围;
的取值范围;②若满足条件的
 点有且只有两个,直接写出
点有且只有两个,直接写出 的值.
的值.
相关试题

