【题目】如图,数轴上![]() 、
、![]() 两点对应的有理数分別为
两点对应的有理数分別为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 分别同时从点
分别同时从点![]() 和点
和点![]() 出发,以每秒
出发,以每秒![]() 个单位长度,每秒
个单位长度,每秒![]() 个单位长度的速度向数轴正方向运动,设运动时间为
个单位长度的速度向数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)当![]() 时,则
时,则![]() 、
、![]() 两点对应的有理数分别是______;
两点对应的有理数分别是______;![]() _______;
_______;
(2)点![]() 是数轴上点
是数轴上点![]() 左侧一点,其对应的数是
左侧一点,其对应的数是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在点![]() 和点
和点![]() 出发的同时,点
出发的同时,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,开始向左运动,遇到点
出发,开始向左运动,遇到点![]() 后立即返回向右运动,遇到点
后立即返回向右运动,遇到点![]() 后立即返回向左运动,与点
后立即返回向左运动,与点![]() 相遇后再立即返回,如此往返,直到
相遇后再立即返回,如此往返,直到![]() 、
、![]() 两点相遇时,点
两点相遇时,点![]() 停止运动,求点
停止运动,求点![]() 运动的路程一共是多少个单位长度?点
运动的路程一共是多少个单位长度?点![]() 停止的位置所对应的数是多少?
停止的位置所对应的数是多少?
参考答案:
【答案】(1)24,8;16;(2)![]() 或10;(3)80;40.
或10;(3)80;40.
【解析】
(1)根据路程=速度×时间,先求出OQ,OP的值,进而可求出PQ的值.
(2)由CB=2CA,可得30-x=2(x-20)或30-x=2(20-x),解方程即可.
(3)设t秒后P、Q相遇.则有4t-2t=20,t=10,此时P、Q、R在同一点,由此可以确定点R的位置.
(1)t=2时,OQ=2×4=8,PA=2×2=4,OP=24,
∴P、Q分别表示24和8,PQ=24-8=16,
故答案为24,8;16.
(2)∵CB=2CA,
∴30-x=2(x-20)或30-x=2(20-x),
∴x=![]() 或10.
或10.
(3)设t秒后P、Q相遇.则有4t-2t=20,
∴t=10,
∴R运动的路程一共是8×10=80.
此时P、Q、R在同一点,所以点R的位置所对应的数是40.
-
科目: 来源: 题型:
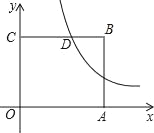
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数
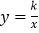 (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.(1)求k的值;
(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划组织师生参加哈尔滨冰雪节,感受冰雪艺术的魅力.出租公司现有甲、乙两种型号的客车可供租用,且每辆乙型客车的租金比每辆甲型客车少60元.若该校租用3辆甲种客车,4辆乙种客车,则需付租金1720元.
(1)该出租公司每辆甲、乙两型客车的租金各为多少元?
(2)若学校计划租用6辆客车,租车的总租金不超过1560元,那么最多租用甲型客车多少辆?
-
科目: 来源: 题型:
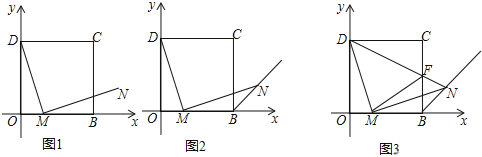
查看答案和解析>>【题目】(1)如图,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标______(用含a的代数式表示);
(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.
(3)在(2)的条件下,如图,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A. 长分别为32,42,52的线段组成的三角形是直角三角形
B. 连接对角线垂直的四边形各边中点所得的四边形是矩形
C. 一组对边平行且另一组对边相等的四边形是平行四边形
D. 对角线垂直且相等的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时 间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
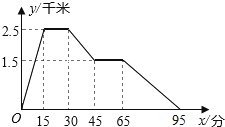
A. 体育场离张强家2.5千米
B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店1.千米
D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在同一直线上,
在同一直线上, ,
,  ,再添加一个条件仍不能证明
,再添加一个条件仍不能证明 
 的是( )
的是( )
A.
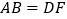 B.
B.  C.
C. D.
D.
相关试题

