【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )
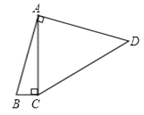
A.10B.8C.12D.20
参考答案:
【答案】A
【解析】
作AE⊥AC,DE⊥AE,两线交于E点,再作DF⊥AC于F点,先证明△ABC与△ADE全等,然后将原四边形面积转化为梯形的面积进一步求解即可.
如图所示,作AE⊥AC,DE⊥AE,两线交于E点,再作DF⊥AC于F点,

则四边形AFDE为矩形,
∴AE=DF,AF=DE,
∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAC=∠DAE,
在△ABC与△ADE中,
∵∠ACB=∠E,∠BAC=∠DAE,AB=AD,
∴△ABC≌△ADE,
∴BC=DE,AC=AE,且△ABC的面积=△ADE的面积,
设BC=![]() ,则DE=
,则DE=![]() ,
,
∵AC=4BC,
∴DF=AE=AC=![]() ,
,
∴CF=ACAF= ACDE=![]() ,
,
在Rt△DFC中,![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴四边形ABCD的面积=△ABC的面积+△ACD的面积=梯形ACDE的面积=![]() ,
,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
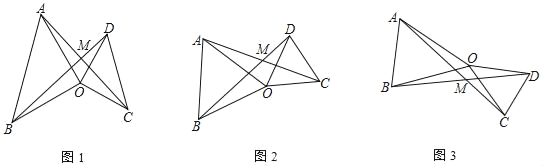
(1)如图1,当α=90°时,∠AMD的度数为 °
(2)如图2,当α=60°时,∠AMD的度数为 °
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,在等边△ABC 中,AD是∠BAC的平分线,一个含有120°角的△MPN的顶点P(∠MPN=120°)与点D重合,一边与AB垂直于点E,另一边与AC交于点F.
①请猜想并写出AE+AF与AD之间满足的数量关系,不必证明.
②在图1的基础上,若△MPN绕着它的顶点P旋转,E、F仍然是△MPN的两边与AB、AC的交点,当三角形纸板的边不与AB垂直时,如图2,(1)中猜想是否仍然成立?说明理由.
③如图 3,若△MPN绕着它的顶点P旋转,当△MPN的一边与AB的延长线相交,另一边与AC的反向延长线相交时,AE、AF与AD之间又满足怎样的数量关系?直接写出结论,不必证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=﹣x+4,y2=
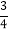 x+b都与双曲线y=
x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式
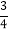 x+b>
x+b> 的解集;
的解集;(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知网格上最小的正方形的边长为
 (长度单位),点
(长度单位),点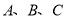 在格点上.
在格点上.(1)直接在平面直角坐标系中作出
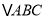 关于
关于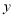 轴对称的图形
轴对称的图形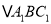 (点
(点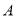 对应点
对应点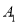 ,点
,点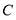 对应点
对应点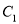 );
);(2)
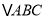 的面积为 (面积单位)(直接填空);
的面积为 (面积单位)(直接填空);(3)点
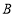 到直线
到直线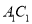 的距离为 (长度单位)(直接填空);
的距离为 (长度单位)(直接填空); 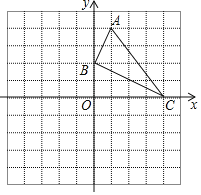
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,以△ABC的边AB为直径作⊙O,交AC边于点E,BD平分∠ABE交AC于F,交⊙O于点D,且∠BDE=∠CBE.
(1)求证:BC是⊙O的切线;
(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,DF=2,求
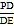 的值及AO的长.
的值及AO的长.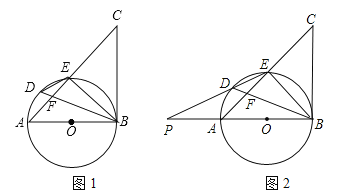
相关试题

