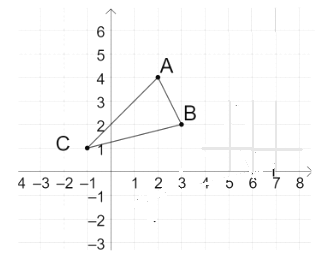
【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 . 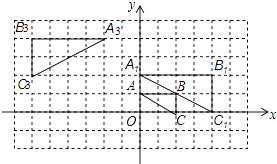
(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
参考答案:
【答案】
(1)![]()
(2)解:如图所示
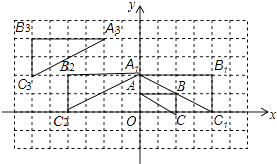
(3)解:△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;
(4)(﹣2x﹣2,2y+2)
【解析】解:(1))△ABC与△A1B1C1的位似比等于= ![]() ;
;
(2)如图所示

(3)△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;
(4)点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为(-2x-2,2y+2).
所以答案是: (1)![]() ;(2)见解答过程;(3)由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;(4)(﹣2x﹣2,2y+2).
;(2)见解答过程;(3)由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;(4)(﹣2x﹣2,2y+2).
【考点精析】利用作图-位似变换对题目进行判断即可得到答案,需要熟知对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A、B、C在同一条直线上,点M为线段AC的中点、点N为线段BC的中点.
(1)如图,当点C在线段AB上时:
①若线段
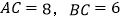 ,求
,求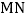 的长度.
的长度.②若AB=a,求MN的长度.
(2)若
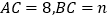 ,求MN的长度(用含
,求MN的长度(用含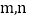 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2017的坐标为( )
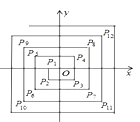
A. (504,504) B. (﹣504,504) C. (﹣504,﹣504) D. (﹣505,504)
-
科目: 来源: 题型:
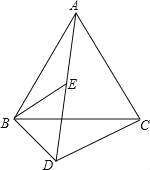
查看答案和解析>>【题目】如图,已知△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明DA﹣DB=DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:
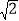 ≈1.41,
≈1.41,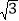 ≈1.73)
≈1.73)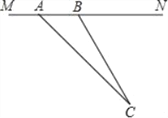
-
科目: 来源: 题型:
查看答案和解析>>【题目】将
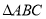 向右平移
向右平移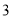 个单位长度,再向下平移
个单位长度,再向下平移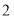 个单位长度,得到
个单位长度,得到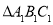
(1)在平面直角坐标系中,画出
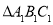 ;
;(2)写出平移后点的坐标:
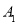 (_____,____).
(_____,____).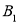 (_____,_____).
(_____,_____). (_____,_____);
(_____,_____);(3)求
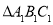 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
相关试题

