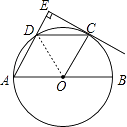
【题目】如图所示,AB是⊙O的直径,点C是 ![]() 的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E 
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
参考答案:
【答案】
(1)证明:
连接OD,如图,
∵C是 ![]() 的中点,
的中点,
∴∠BOC=∠COD=60°,
∴∠AOD=60°,且OA=OD,
∴△AOD为等边三角形,
∴∠EAB=∠COB,
∴OC∥AE,
∴∠OCE+∠AEC=180°,
∵CE⊥AE,
∴∠OCE=180°﹣90°=90°,即OC⊥EC,
∵OC为圆的半径,
∴CE为圆的切线
(2)解:
四边形AOCD是菱形,理由如下:
由(1)可知△AOD和△COD均为等边三角形,
∴AD=AO=OC=CD,
∴四边形AOCD为菱形.
【解析】(1)连接OD,可证明△AOD为等边三角形,可得到∠EAO=∠COB,可证明OC∥AE,可证得结论;(2)利用△OCD和△AOD都是等边三角形可证得结论.
【考点精析】通过灵活运用菱形的判定方法和切线的判定定理,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.

(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,当△ABC为正三角形时,点E是否AC的中点?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市,l1 ,l2分别表示汽车、摩托车离A地的距离s(km)随时间t(h)变化的图象,则下列结论:①摩托车比汽车晚到1 h;②A,B两地的距离为20 km;③摩托车的速度为45 km/h,汽车的速度为60 km/h;④汽车出发1 h后与摩托车相遇,此时距离B地40 km;⑤相遇前摩托车的速度比汽车的速度快.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围. -
科目: 来源: 题型:
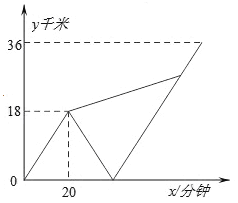
查看答案和解析>>【题目】甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)电动车的速度为 千米/分钟;
(2)甲步行所用的时间为 分;
(3)求乙返回到学校时,甲与学校相距多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
B.
C.
D.
相关试题

