【题目】国庆节放假时,小华一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,向东走了4千米到超市买东西,然后又向东走了3千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
(2)问超市A和外公家C相距多少千米?
(3)若小轿车每千米耗油0.09升,求小明一家从出发到返回家所经历路程小车的耗油量.(精确到0.1升)
![]()
参考答案:
【答案】(1)图形见解析(2)9(3)2.2
【解析】
试题(1)从家向东走了4千米到超市,即从0向右4个单位长度,则超市A表示4,又向东走了3千米,即从4向右3个单位长度,则爷爷家B表示的数为7,从爷爷家出发向西走了12千米到外公家,即从7向左12个单位长度;(2)右边的数减去左边的数即可;(3)计算总路程,耗油量=总路程×0.09.
解:(1)A为0+4=4,B为4+3=7,C为7-12=-5,在数轴上表示为:
![]()
(2)A表示4,C表示-5,
4-(-5)=9(千米).
答:超市A和外公家C相距9千米;
(3)行走总路程为4+3+12+5=24(千米),
24![]() 0.09=2.16≈2.2(升).
0.09=2.16≈2.2(升).
答:小明一家从出发到返回家时小车的耗油量约为2.2升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的角平分线CF于点F,求证:AE=EF.

经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】读一读:式子“1+2+3+4+5+……+100”表示从1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可将“1+2+3+4+5+……+100”表示为
 ,这里“
,这里“ ”是求和符号.例如:“1+3+5+7+9+……+99”(即从1开始的100以内的连续奇数的和)可表示为
”是求和符号.例如:“1+3+5+7+9+……+99”(即从1开始的100以内的连续奇数的和)可表示为 ;又如“13+23+33+43+53+63+73+83+93+103”可表示为
;又如“13+23+33+43+53+63+73+83+93+103”可表示为 .同学们,通过对以上材料的阅读,请解答下列问题:
.同学们,通过对以上材料的阅读,请解答下列问题:①2+4+6+8+10+……+100(即从2开始的100以内的连续偶数的和)用求和符号可表示为 ;
②计算:
 = (填写最后的计算结果).
= (填写最后的计算结果).③求:
 的值.(写出必要的过程)
的值.(写出必要的过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:

(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则原方程化为y2﹣5y+4=0,解此方程得:y1=1,y2=4.
当y=1时,x2﹣1═1,∴x=±
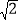 .
.当y=4时,x2﹣1═4,∴x=±
 .
.∴原方程的解为:x1=
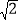 ,x2=﹣
,x2=﹣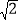 ,x3=
,x3= ,x4=﹣
,x4=﹣ .
.以上方法叫做换元法解方程,达到了降次的目的,体现了转化思想.
运用上述方法解方程:x4﹣8x2+12=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
相关试题

