【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.

(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
参考答案:
【答案】(1)见解析;(2)成立,见解析
【解析】
试题分析:(1)根据平行四边形的性质可得AO=CO,BO=DO,再由条件点E、F分别为BO、DO的中点,可得EO=OF,进而可判定四边形AECF是平行四边形;
(2)由等式的性质可得EO=FO,再加上条件AO=CO可判定四边形AECF是平行四边形.
(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵点E、F分别为BO、DO的中点,
∴EO=OF,
∵AO=CO,
∴四边形AECF是平行四边形;
(2)解:结论仍然成立,
理由:∵BE=DF,BO=DO,
∴EO=FO,
∵AO=CO,
∴四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=70°.在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )

A.30° B.35° C.40° D.50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知抛物线y=k(x+1)(x﹣3k)(且k>0)与x轴分别交于A、B两点,A点在B点左边,与Y轴交于C点,连接BC,过A点作AE∥CB交抛物线于E点,0为坐标原点.
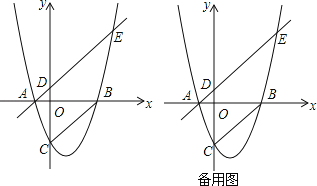
(1)用k表示点C的坐标(0, );
(2)若k=1,连接BE,
①求出点E的坐标;
②在x轴上找点P,使以P、B、C为顶点的三角形与△ABE相似,求出P点坐标;
(3)若在直线AE上存在唯一的一点Q,连接OQ、BQ,使OQ⊥BQ,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.
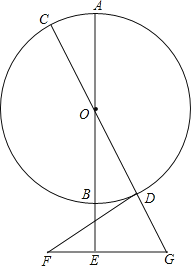
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )
A.(﹣3,﹣6)
B.(1,﹣4)
C.(1,﹣6)
D.(﹣3,﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2+8x+7=0,则方程可化为( )
A. (x+4)2=9 B. (x﹣4)2=9 C. (x+8)2=23 D. (x﹣8)2=9
相关试题

